2 + 2 = 4(?)
Et meme si ce nest, pas vrai, faut croire a I'histoire ancienne.
[Even if it's not true, you must believe in ancient history.]
~Leo Ferre
The man, the myth...
As you may have noticed, developments in mathematics have accompanied great intellectual breakthroughs in the past. It's even the case that various of the philosophers we've covered were themselves accomplished mathematicians—or they at least tried to stay up-to-date with developments in the field. Moreover, it really does seem to be the case that a field of inquiry (i.e., a discipline one studies, such as astronomy, psychology, history, etc.) seems to mature as it becomes mathematized (Turchin 2018). And so, what we're about to do will seem paradoxical: we are going to question mathematics.

As a sort of method of warming you up to this, I want to introduce you to the work of the mathematician and historian of mathematics Alberto Martínez (2012). In his book The Cult of Pythagoras, Martínez attempts to dispel many of the myths in mathematics. He begins with a mathematical legend: Pythagoras. Let's begin with a question. What do we actually know about the historical Pythagoras? Well, we know that Pythagoras was probably a real person. And we know that in the 6th century BCE various communities based on his teachings and beliefs originated and spread through Magna Graecia, which is how the Romans referred to southern Italy. We also know that, due to political instability in Italy, most Pythagorean communities had left Magna Graecia by 400 BCE, and that some of these refugees regrouped in Greece. And, according to Martínez, that's about it. All other "facts" that you think you know about Pythagoras are pure speculation.
Let's return to the Pythagorean communities (that we know with certainty existed) to see what Martinez means. Around 400 BCE, these communities were now at least a century removed from the historical Pythagoras, and so there were disputes as to how to interpret his teachings. There were two main factions. One stressed renunciation of material wealth. The other faction, the mathēmatikoi, focused on Pythagoras' "scientific" claims: his interpretations of the world and how best to understand it. Both factions, however, appeared to believe incredible things about their teacher.
Myths attributed to Pythagoras:
- He never laughed.1
- He infallibly predicted earthquakes, storms, and plagues.
- He was so charismatic that every day almost the entire city turned to him, as if he were a god.
- He once spoke to a river while crossing it and the river responded, "Hail, Pythagoras!"
- He was the son of Apollo.
See (Martínez 2012: 2).
Perhaps most famously, in addition to these myths, Pythagoras was said to have personally made various mathematical discoveries. But even this has now come to be questioned, not to mention the unbelievable myths described above.
“In the end, what can we attribute to the Pythagoras (as opposed to contemporaries who shared his name) with certainty in the history of mathematics? Nothing. As argued by historian Walter Burkert, ‘The apparently ancient reports of the importance of Pythagoras and his pupils in laying the foundations of mathematics crumble on touch, and what we can get hold of is not authentic testimony but the efforts of latecomers to paper over a crack, which they obviously found surprising’... Historian Otto Neugebauer briefly remarked that the stories of Pythagoras’s discoveries ‘must be discarded as totally unhistorical’ and that any connection between early number theory and Pythagoras is ‘purely legendary and of no historical value’” (Martínez 2012: 14).
There are various things that I should point out here. If your early education was anything like mine, you were taught that Pythagoras was a mathematician, and his religious teachings were seldom mentioned, if ever. At least in my case, I don't recall being taught these myths about the historical figure. I certainly don't think that I was told that his followers considered him divine. Moreover, something about this doesn't sit well. Mathematics seems linked in a fundamental way to science, not to religion. Nevertheless, we have seen this time and time again. Thinkers from the past have married their mathematical pursuits with their religious convictions. Newton, Copernicus, Brahe, Kepler, Pascal, Galileo, Descartes, and Leibniz were all believers, and some of these saw their mathematical work as a religious task: an attempt to speak the language of God. Do you see what's going on here? Mathematics seems to somehow be imbued with a supernatural element.
None of this, of course, is to say that mathematics is not a worthwhile endeavor. Mathematics is both fascinating and shockingly useful. It boggles the mind that, for example, linear algebra—developed centuries before digital computers—ended up being useful for machine learning (not to mention quantum mechanics). Ditto for Boolean algebra. Non-Euclidean geometry, developed in the 1800s, is the language of Einstein's relativity theory, developed in the 1900s. And one can go on and on. However, there is something mystical about mathematics, and it can be seen from the very beginning in these Pythagorean communities which persisted and whose ideas spread...

The worship of numbers
Even though his 2012 book is only partially about Pythagoras, Martínez still named it The Cult of Pythagoras. This is because Martínez claims that mathematicians (like himself):
-
have a quasi-divinical approach to mathematics, either believing that they have a special sense that allows them to glimpse into the realm of mathematical truth, or they claim that some deity helps them discover mathematical theorems, or they believe triangles are somewhat supernatural in that they have existed before humans and will continue to exist after humans;
-
(like some religions) are guilty of embellishing their own history; and
-
(like some religions) have a track-record of brushing their past conflicts under the rug.
Martínez gives plenty of evidence for his claims from the history of mathematics, but I'd like to share two datum in particular. First, in 2001, the magazine Physics World ran a poll on the philosophical views of physicists. Among various questions (about the reality of electrons, genes, atoms, lightwaves, etc.), the survey also asked about beliefs regarding numbers. Two-thirds of the respondents claimed that real numbers (a value that represents any quantity along a number line) are "real"; 43% claimed that imaginary numbers (like √-1) are real as well. Martínez also surveyed his students each semester from 2005 to 2010. “Out of 245 majors in mathematics and the sciences over those five years, 77 percent of the students wrote that triangles existed before humans and will continue to exist forever. Almost 22 percent disagreed, and only 3 students chose not to reply and wrote instead ‘maybe,’ ‘neither,’ or ‘no idea’” (Martínez 2012: xx). Clearly students of mathematics and related disciplines believe there is something "special" about numbers, that they exist in a way independent of human minds.
Anyone with knowledge of the history of mathematics can recall other important figures who shared this quasi-divinical treatment of numbers. Take for example, legendary mathematician Kurt Gödel...
“The most commonly cited remark of Gödel’s on this topic involves a direct claim that [mathematical] intuition is ‘something like a perception’ of mathematical objects… Gödel believed not just that human minds are immaterial… but that we are led to this conclusion by reflecting on mathematics’” (Balaguer 2001: 27).
John Nash, who made fundamental contributions to game theory—such as the concept of the Nash equilibrium—and who was played by Russell Crowe in A Beautiful Mind, similarly claimed a sixth sense for mathematical intuition, a sense which wouldn't allow him to distinguish between his mathematical ideas and the onset of schizophrenia.
“‘How could you’, began [Harvard Professor George] Mackey, ‘how could you, a mathematician, a man devoted to reason and logical proof… how could you believe that extraterrestrials are sending you messages? How could you believe that you are being recruited by aliens from outer space to save the world? How could you…?’... ‘Because’, Nash said slowly in his soft, reasonable southern drawl, as if talking to himself, ‘the ideas I had about supernatural beings came to me the same way that my mathematical ideas did’” (Previc 2009: 69).
Mathematician and historian of mathematics Jeremy Gray reminds us that many great mathematicians, including Carl Friedrich Gauss, were "addicted to the calculation of examples" (Gray 2003: 135). This is not unlike the repetitive nature of some chants and prayers, like Buddhist chants and the saying of the Rosary.
Lastly, Indian math savant Srinivasa Ramanujan (1887-1920) claimed to receive his mathematical intuitions from a goddess. Ramanujan is the subject of the film The Man Who Knew Infinity.
If these great thinkers thought mathematics worthy of this near-worship, should we do the same?
Food for thought...

Important Concepts
On truth
As you learned in the Important Concepts above, there is some disagreement on what truth is. In fact, we discussed this briefly all the way back in Lesson 1.2 Agrippa's Trilemma. Recall that we were distinguishing between epistemology, the branch of philosophy concerned with the nature and limits of knowledge, and metaphysics, the branch of philosophy concerned with the nature of reality. Recall also that there is considerable overlap between these branches. For example, a quintessential question in epistemology is: How do we come to know which statements are true? A related metaphysical question is: What is truth? Notice that the first question (“How do we come to know which statements are true?”) is equivalent to asking what the right method for acquiring true beliefs is, not what truth itself is. “How do we come to know which statements are true?” is a question about what the best belief-forming practices are. “What is truth?” is asking about what all true statements have in common. Clearly there is overlap between the two branches, but they’re still not the same question.
Whereas when we kicked off this course, we focused on the epistemic side of things, let's circle back and think about metaphysics. The metaphysical question above is particularly strange. What is truth? The question almost seems poorly formed. I think that an approach to thinking about truth which was developed in the 20th century is helpful here. Some philosophers began to think about truth not as a physical thing (as in "the whole truth", whatever that means) or a place (as in "getting to the truth"), but rather as a property. In particular, it is a property of declarative sentences.
Some declarative sentences have this property called truth. For example, "Sacramento is the capital of California" enjoys having the property of being true. Other declarative sentences, however, lack this property of truth. For example, "R.C.M. García is a millionaire" is (unfortunately) not true. What do these true sentences have in common? Philosophers came up with the concept of a truthmaker, i.e., something that makes the statement true. What counts as a truthmaker ranges widely, depending on the context. For example, "Sacramento is the capital of California" is true due to some legal fiction. If you go to Sacramento, you won't find the property capital anywhere; rather, Sacramento is the capital of California by virtue of an agreed upon legal framework. Other statements, like "The cat is on the mat" depend on the state of physical things, such as whether or not whatever cat is being referred to is actually on whatever mat is being referred to. Sometimes you might say that there's a combination of truthmakers, as in "The cat is in the capital of California".
Be careful, though. Only a proposition, or the thought expressed by a declarative sentence, has a truthmaker. This might be tough to get a grasp on first, so let me give you some examples. Consider the following set of sentences:
- "Snow is white."
- "La neige est blanche."
- "La nieve es blanca."
- "Schnee ist weiß."
This set contains four sentences. That's clear enough. But how many propositions does it contain? In fact, it is only one proposition. This is because this is the same thought expressed in four different languages. These sentences, moreover, are clearly different from sentences like "What’s a pizookie?", "Close the door!", and "AHH!!!!!". It just simply is the case that we cannot reasonably apply the label of true or false to a question ("What’s a pizookie?"), a command ("Close the door!"), or an exclamation ("AHH!!!!!"), the way we can to a declarative sentence. As such, non-propositions are simply neither true nor false; they are said to lack truth-functionality.
And so, with the preliminaries out of the way, here is the question: what is the truthmaker of true mathematical statements? In other words, what makes “2 + 2 = 4” true? Notice that we are not denying that “2 + 2 = 4” is true—at least not yet. What we are wondering about is what it is that makes the statement true. We are looking for its truthmaker.
Decoding PHIL of Math
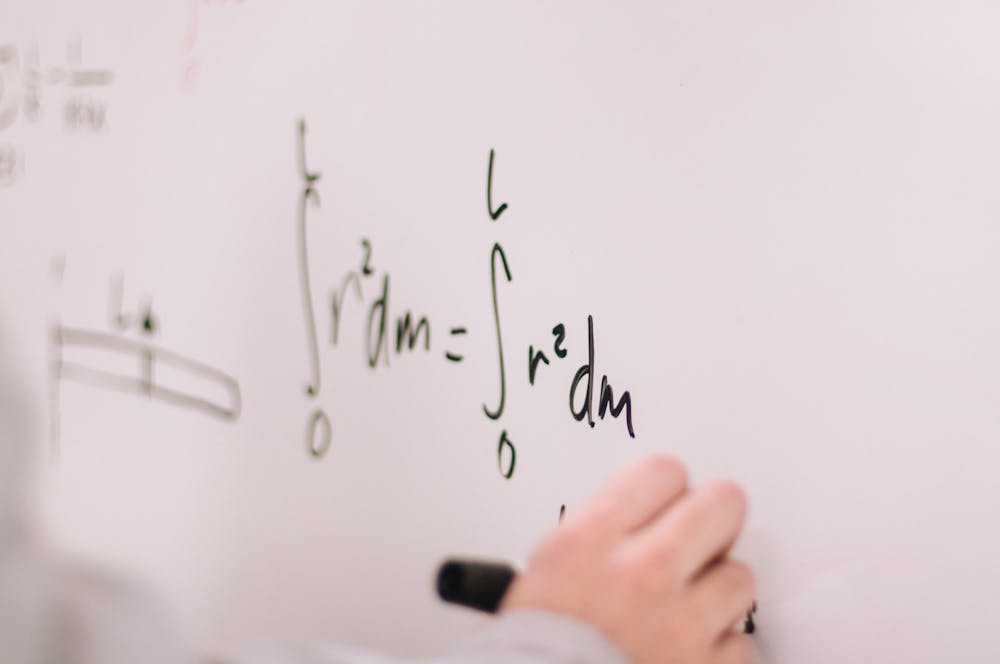

The thing about mathematical truth...
It is difficult to understate how different our modern conceptions of mathematical truth are from those of thinkers from the past, namely thinkers before the dawn of non-Euclidean geometry. This is not the place to get into the technical details of geometry, whether it be Euclidean or non-Euclidean, so instead I'll focus on what theorists thought about geometry. Perhaps the best example of pre-non-Euclidean thinking is none other than Immanuel Kant—again. Recall that Kant argued we can make synthetic a priori judgments, i.e., judgments whose justification is independent of experience but that are objectively true about things-in-themselves (the world itself). And recall also that one of his principal examples is (Euclidean) geometry. In other words, not only is geometrical truth known with absolute certainty, but it allows us to discover new facts about the world (things-in-themselves).
“The mathematics of space (geometry) is based upon this successive synthesis of the productive imagination in the generation of figures. This is the basis of the axioms which formulate the conditions of sensible a priori intuition (from which it can be shown) that two straight lines cannot enclose space" (Kant as quoted in Gray 2003: 84).
However, Kant was not the only thinker that felt this way. All scientists, philosophers, and anyone that had any thoughts on geometry believed that geometry yielded absolute truth. And this belief was shattered in the 19th century, as non-Euclidean geometries began to be developed and accepted. No one puts the point more clearly than mathematician and historian of mathematics Morris Kline:
“In view of the role which mathematics plays in science and the implications of scientific knowledge for all of our beliefs, revolutionary changes in man’s understanding of the nature of mathematics could not but mean revolutionary changes in his understanding of science, doctrines of philosophy, religious and ethical beliefs, and, in fact, all intellectual disciplines...The creation of non-Euclidean geometry affected scientific thought in two ways. First of all, the major facts of mathematics, i.e., the axioms and theorems about triangles, squares, circles, and other common figures, are used repeatedly in scientific work and had been for centuries accepted as truths—indeed, as the most accessible truths. Since these facts could no longer be regarded as truths, all conclusions of science which depended upon strictly mathematical theorems also ceased to be truths... Secondly, the debacle in mathematics led scientists to question whether man could ever hope to find a true scientific theory. The Greek and Newtonian views put man in the role of one who merely uncovers the design already incorporated in nature. However, scientists have been obliged to recast their goals. They now believe that the mathematical laws they seek are merely approximate descriptions and, however accurate, no more than man’s way of understanding and viewing nature” (Kline 1967: 474-75).
What is non-Euclidean geometry? An example of the various types of non-Euclidean geometries is the geometry of curved space which was eventually used in relativity theory. You can watch this lecture on the history of non-Euclidean geometry for more information. There's also a cool demo in the Related Material below.
All this is to say that the fact that there are counterintuitive implications to nominalism/fictionalism does not discount the theory. Some mathematicians explicitly endorse this view (Field 2016). They accept that mathematics is a formal language that we've invented. It's like a game with rules that we've specified, and we happen to have specified those rules such that they are useful to us in interacting with the physical world.
Comments on abstract objects
As we saw, some philosophers and mathematicians have a very different perspective about mathematical objects. They argue that: a. mathematical objects do exist objectively (i.e., they are real), and b. they are non-physical, abstract objects that exist independently of the mind. This to say that mathematical objects exist in a non-physical, mind-independent way. On this view, mathematical objects existed before humans and will exist once we're gone too. These mathematical objects are said to exist in some other plane of existence; it wouldn't be too much of a stretch if we say that they reside in another dimension. But, just like Gödel claimed, we can access these abstract objects through the use of reason (or some kind of mathematical intuition).
Non-physical, mind-independent objects are difficult to wrap your mind around. They are difficult to describe since they are not physical, but, importantly, they're also not things we made up—allegedly. If you want something to compare it to, an abstract object is like what a soul is—if you believe in souls. Another analogy is to God—if you believe in God. The idea here is that God isn't physical or bound by time. He's always existed and always will, which is what some mathematicians believe about numbers, triangles, etc. You learn more about these in the TL;DR.
How do we come to know these abstract objects? As previously mentioned, some mathematicians and philosophers claim that we have a special mathematical intuition for grasping mathematical truth. This view, I might add, isn't completely crazy. There are cases of extraordinary ability to perform mathematical calculations in minds that perform below-average in basically every other domain. In other words, there are people who perform amazing mathematical feats but are mentally disabled. In his book The Number Sense, Dehaene discusses these so-called "idiot savants." In one case, a subject named "Michael" is described as a "profoundly retarded autistic" young man. His verbal IQ cannot even be measured. Nonetheless, Michael can instantly see that 627 can be decomposed into 3×11×19. It takes Michael a little more than a second to assess whether a three-digit number is prime or not; it took a scholar with a math degree ten times that amount of time to perform the same task. Dehaene also reminds us that neurologist Oliver Sacks reports that he once caught two autistic twins exchanging very large prime numbers (see Dehaene 1999: 144-72). Can these individuals "see" numbers in a different way than the rest of us? Did Gödel "see" numbers in this way too? It is true that there is a tight link between mathematical and spatial aptitudes: the higher your spatial intelligence, the higher your aptitude for mathematics (Hermelin and O'Connor 1986). Do numbers exist independent of the human mind and are some minds capable of seeing into this mathematical realm?
The view that mathematical objects are non-physical and mind-independent, by the way, is called Platonism about mathematics. It's called this since it is the view of Plato...

To be continued...
FYI
Suggested Reading: Mark Balaguer, Stanford Encyclopedia of Philosophy Entry on Platonism in Metaphysics Sections 1, 2, 3, and 4.1
TL;DR:
-
Video: Closer to Truth, Is Mathematics Eternal?
-
Video: Closer to Truth, Is Mathematics Invented or Discovered?
Supplemental Material—
-
Video: TEDTalks, What are numbers? | Kit Fine
-
Video: Philosophy Overdose, Intro to the Philosophy of Mathematics (Ray Monk)
Related Material—
Video: CodeParade, Non-Euclidean Worlds Engine
Footnotes
1. Interestingly, it's possible that what we think about the appropriate context and reasons for smiling and laughter are not at all what the ancients believed. Read Mary Beard's Laughter in Ancient Rome: On Joking, Tickling, and Cracking Up for a study of how modern day humor differs from ancient humor.

