Rules of Inference
(Pt. I)

Logic and mathematics seem to be the only domains where self-evidence manages to rise above triviality; and this it does, in those domains, by a linking of self-evidence on to self-evidence in the chain reaction known as proof.
~W. V. O. Quine
Approaching modern logic...
At this point, you are familiar with both Aristotelian and Stoic logic, as well as some of their methods of assessing for validity. In addition to the informal Imagination Method (where you simply use your logical intuition to see if a conclusion is necessitated by the premises), you've also seen Aristotle's Square of Opposition at work on immediate inferences, as well as the method of assessing for validity which makes use of a syllogism's mood and figure, a method which Aristotle also pioneered. We've also seen the Stoic's method of pattern recognition and truth-table analysis which was developed in 1893 by C. S. Peirce (see Anellis 2012). The approach we've taken has been more or less historical, beginning with ancient techniques first and then jumping to the 19th century—a sliding timeline technique we used both for Aristotle's categorical logic and for Stoic truth-functional logic.1
We are now moving towards a method that was first developed in the 1930's (see Pelletier 1999). As you will soon see, this method clearly needed to wait until logicians had a formal language through which they could reduce very complicated expressions into a few symbols. We will be utilizing TL to this end. It is called natural deduction.
Before we move into natural deduction, however, it is important to lay out some questions that might arise at this juncture. Some of these questions, although they seem trifling at first, tie into other innovations of the 20th century—innovations that changed the world. Although logic's part in the digital revolution is just one of many key innovations that allowed the revolution to happen, a student of computer science will quickly recognize in some of the techniques we'll be learning the similarities to writing computer code.
Here are some questions that we might ponder at this point:
- Aristotle or the Stoics? Once logicians had a formal language for logic, first-order logical systems were proven to be truth-functionally complete and truth-functionally consistent. But the question is: Under whose terms? Is the right approach to logic categorical or truth-functional? Both logics are "contained" within modern first-order logic, but who acquired who?
- Can we symbolize Aristotle and Boole? At the end of Unit I we were left with the puzzle of logical relativity: some arguments were valid depending on whether we took the hypothetical viewpoint or the Aristotelian existential viewpoint. But we had no way of expressing this distinction in our symbols. Is there a way to do this?
- Is Logicism true? Recall that Frege's impetus for developing his formal language was to demonstrate that mathematics can be derived out of logic. Is this possible?
- How do we know Stoic valid argument forms are actually valid? We used the Stoic pattern recognition method in the last unit, but can we prove that they are actually always valid?

Actually...
We can answer one of the questions above now. We've already done it with truth-tables, and, even though there are more formal methods, this shows us that there really is something special about these patterns of thought. They do appear to be always valid. Here's a slideshow to remind you of the tables in question.
We can also begin to address question #1 above. It really does seem like categorical logic and truth-functional logic are similar enough to unify. Here's one similarity. Notice that in modern categorical logic, we draw a Venn diagram for an argument and then populate it with information from the argument, namely the premises. In modern truth-functional logic, we draw a truth-table for an argument, then we populate it with information from the argument. Only then do we decide if the argument is valid or invalid.
Another similarity is that the validity tests for both are visual. If you've correctly populated the information from a valid argument into a Venn diagram, you can literally see the conclusion. Something similar occurs in truth-table analysis—you can see the validity (or non-validity) of the argument.
Lastly, both validity tests are mechanical. They are algorithmic. There are steps one must follow. In other words, when assessing for validity, we become like human computers. In fact, when we follow algorithmic processes to assess for validity, we are doing what modern computers do when they read parameters for customized programs. Tellingly, parameters are also known as arguments.
For these reasons it seems at least possible that we can unify categorical logic and truth-functional logic. But will it be under Aristotelian or Stoic terms? Stay tuned.


Important Concepts

Food for thought...
As previously stated, in Chapter 6 of A Mind for Numbers, Barbara Oakley reminds us that “choking” occurs when we have overloaded our working memory. To prevent this from happening, we must take enough time to “chunk”, or integrate one or more concepts into a smoothly connected working thought pattern. Put another way chunking is the mental process of grouping together connected items, words, or even whole declarative sentences so that they can be stored or processed as single concepts.
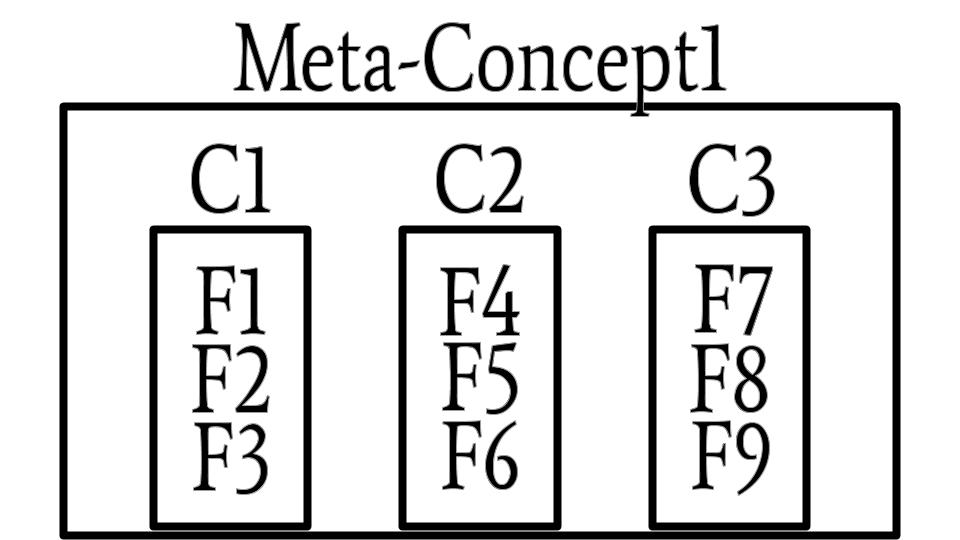
Metaconcept diagram.
In order to become proficient in natural deduction, you'll need to truly integrate the rules of inference so that you can easily recognize them "in the wild". This will require that you learn how to chunk. The idea is simple enough. Take a look at the diagram on the right. The idea is that concepts are made of facts. For example, Concept 1 (C1) is composed of Fact 1 (F1), Fact 2 (F2), and Fact 3 (F3). Once you've chunked F1, F2, and F3 into C1, you've substantially lessened the load on your working memory. You can perform this feat at a higher level by chunking several concepts into a metaconcept. In the diagram, Metaconcept 1 is composed of Concept 1 (C1), Concept 2 (C2), and Concept 3 (C3).
In the days to come you must memorize the rules of inference. It is absolutely essential, since no student is successful in natural deduction without having these rules well-integrated into their working memory. To actually enjoy natural deduction, you'll need to be able to see how a combination of rules can help you complete a proof. In other words, these combinations will be like metaconcepts. I liken this to a combination of moves on the chessboard that you know are typically successful. You can also think about it as gears working together. One gear alone doesn't make a clock tick. But there is a beauty to the gears working together in concert to perform a function. But only the clockmaker knows the necessary pattern. It's time to start looking for patterns.


Rules of Inference


Storytime!
You might have noticed that one of the rules of inference discussed in the video was the Stoic argument form modus ponens. This is not all that Stoics have handed down to us. In fact, the Stoics are mostly known for their ethical views.

Bust of
Marcus Aurelius.
In his inspiring 2019 How to Think Like A Roman Emperor, Robertson reminds us that, although Academic Philosophy today is stuffy and esoteric, Philosophy in the ancient world was much more a way of life. It appears to be the case that you could identify philosophers by the way they looked. The Stoics were no exception. Even the most powerful Stoic to have ever lived, the Roman emperor Marcus Aurelius, only reluctantly wore his royal garbs, after being much pressured by his advisors.
Although most Stoic writings are lost (see Footnote 1), we can discern their basic view: you just live in accordance with nature. This was synonymous with living wisely and virtuously. The Greek word arete, the ultimate aim of a Stoic's life, is actually best translated not as “virtue” but as “excellence of character.” Something excels when it performs its function well. Stoics believed that humans excel when they think clearly and reason well about their lives. The Stoic cardinal virtues are wisdom, justice, courage, and moderation, a set of virtues that was co-opted from the Platonic school. The Stoics stressed that arete is the only intrinsic good. External factors, like fancy clothes, wealth, and social status, are only advantages, not goods. They have no moral status. The wise mind uses them to achieve arete.
Perhaps the most important contribution of the Stoics to Western thought, logic notwithstanding, was the concept of logos. The Stoics theorized that there was an all-pervasive cosmic force that organized everything rationally. This is the logos. This notion was the reason that the Stoics were the first philosophers in history to argue for what today we would call human rights. This is since humans exhibited rationality (at least sometimes). But logos is itself rational. This must mean, Stoics reasoned, that each of us contains a spark of this divine logos. And so, we are all worthy of dignity and respect.2

FYI
Homework!
Footnotes
1. As previously noted, Stoic writings, along with most of the literature of the classical world, are lost, a process that was initiated when Christians took control of the Roman empire in the 4th CE (Nixey 2018). In fact, only about 10% of classical writings are still in existence. If one narrows the scope only to writings in Latin, it is only about 1% that remains (ibid., 176-177; see also Edward Gibbon's History Of The Decline And Fall Of The Roman Empire, chapters 15 and 16). And so, Stoic logic was actually reconstructed (or "rediscovered") in the 20th century, as modern logicians were formalizing their field (O'Toole and Jennings 2004). A key figure in this reconstruction was Benson Mates, whose 1972 Elementary Logic I cited when describing the history of logic back in Unit I.
2. So important was the notion of logos that it was even incorporated into Christianity. It appears early on in the Gospel of John, but it is developed further by the so-called Doctors of the Church. The reason for this is interesting. Apparently, the register and accent that the various books of the Bible were written in tended to grate on educated ears. In short, it was “embarrassing” to many Christian intellectuals that texts allegedly inspired by God were written in a less than glorious style (Nixey 2018: 160-61). So full of grammatical mistakes and inelegant prose (at least compared to pagan writers) was the Bible that St. Augustine even felt the need to defend it (ibid.; see also Brown 1967: 458). Given the obvious superiority of pagan literature, argues Nixey, Christians began to Christianize and absorb it, at least in part due to self-interest: to raise the intellectual caliber of the Church. But it was only the parts that could be fit into existing Christian dogma. And so, some Greek concepts, like that of logos, found their way into Christian philosophy. Needless to say, writings that did not serve Christianity any useful function were either neglected or deliberately destroyed and eventually lost to history.

