Rules of Inference
(Pt. III)

 

 

Absurdity and Truth

Question: Have you ever wondered why contradictions are so frowned upon? Of course, contradictions are bad. Everyone knows this. But can you prove that they are absurd? Now you can.

If you begin with a contradiction as an assumption, you can literally deduce anything. For example, in the argument below, let's take "A" to represent "RCG plays piano". Let's also blatantly contradict ourselves and open with the assumption "A & ~A". Using the simple tilde elimination rule, you can easily establish that "B" naturally follows from this assumption (see derivation below). But "B" could be anything!

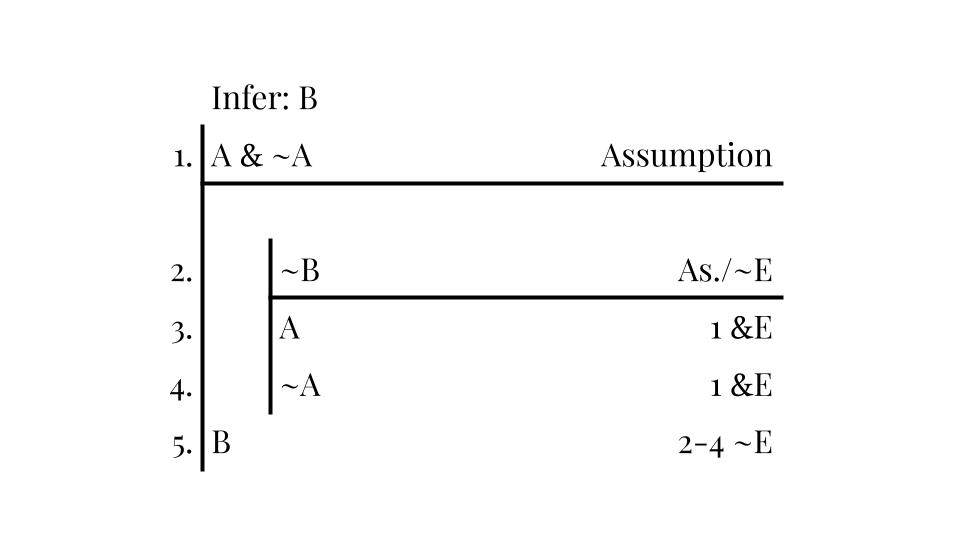
This shows that if someone accepts even one contradiction as true, then any sentence can validly follow. In other words, if even one contradiction is true, then every sentence is true. This collapses the distinction between truth and falsity. But this is completely absurd. The functionality of our language, both TL and our natural languages, requires the basic distinction between truth and falsity. The only solution is to stipulate that contradictions cannot be. This is called the Law of Noncontradiction (for analysis, see Herrick 2013: 388-9).

 

 

 

Important Concepts

 

Clarifications on the different flavors of natural deduction...

As you learned in the Important Concepts above, we will be building various types of proofs. Fundamental to understanding these is the notion of derivability, the general idea being that a sentence P of TL is derivable from a set of sentences Γ if you can derive P by the use of a finite number of inference rules from the set Γ.

One type of derivation we can perform is to demonstrate that an argument is valid. The setup for this is to set the premise(s) of the argument as the initial assumption(s) and then derive the conclusions using valid inference rules. If this can be done, then the argument is valid. In this unit, I will only give you valid arguments. Your task will be to show the valid inference rules that take us from the premises to the conclusion.

You will also be asked to prove theorems. These are derivations in which there are no initial assumptions. Put more formally, a sentence P of TL is a theorem in SD if, and only if, P is derivable in SD from the empty set. In practice, this means that you must draw your main scope (as always), place the theorem to be proved at the bottom of the scope line, and then begin immediately with some subderivational rule. A good rule of thumb is to look at the main operator of the theorem to be proved and use a rule relating to that operator. For example, if the theorem is a conditional, you're most likely going to use conditional introduction. If all else fails, use one of the tilde rules. When you are asked to do problems of this sort, rest assured that the sentences in question will in fact be theorems. Your task will be to prove that they are.

One last derivation that we will be performing is the proof of inconsistency. The general idea is that you will show some set of sentences Γ to be inconsistent by deriving a contradiction on the main scope. When you are asked to do problems of this sort, you will be assured that the set is in fact inconsistent. Your task will be to derive a contradiction.

Note on symbols

I should add one more thing. Previously we had been using the double turnstile ("⊨") to mean logical consistency. Now that we've developed our formal language, we can be more precise. We will use the "⊨" symbol to mean semantic entailment. For example:

{"Rodrigo weighs 200lbs."} ⊨ "Rodrigo weighs more than 100lbs."

In this example, the meaning of the sentence in the set ("Rodrigo weighs 200lbs.") entails the meaning of "Rodrigo weighs more than 100lbs." In other words, accepting the truth of the meaning (or semantic content) of the first guarantees that you will accept the truth of the semantic content in the second.

This same notion should carry over to our formal language TL. We will use the single turnstile ("⊢") to mean syntactic entailment. These two concepts, we hope, should be isomorphic. That is to say, relationships of semantic entailment in natural language should carry over as syntactical entailment in formal languages. Here's an example of a set syntactically entailing another sentence in TL:

{~(A & B), A} ⊢ ~B

Put in the simplest terms, we'll be using "⊨" when using natural language and "⊢" when using TL.

 

 

 

Slow burn...

We have now entered the most frustrating (but rewarding!) part of the course. Believe it or not, the method of proof that we are using is much more user-friendly than previous systems. That's actually why it's called "natural deduction." But these "natural deductions", our derivations, take some getting used to either way. You must learn to "see" the patterns of reasoning, follow the inference rules rigorously, and double check your work to ensure you have not made any illegal moves or syntax errors. To be honest, it will be tough in the beginning. Here are some tips.

In chapter 2 of A Mind for Numbers, Oakley gives the following tips for working on tough math problems:

• When doing focused thinking, only do so in small intervals (at first). Set aside all distractions for, say, 25 minutes. Use a timer.
• Focus not necessarily on solving the problem, but do work diligently to make progress.
• Then when your timer goes off, reward yourself.
• Try to complete 3 of these 25min intervals any given day.

In chapter 3, Oakley emphasizes that breaks are essential. Surf the web, take a walk, workout, switch to a different subject. Your mind will naturally keep working on the problem in the background. But(!) have a paper and pen handy. Solutions may come at any time. And don’t stay away from a problem for longer than a day. You might lose your progress, just like in physical fitness.

I have to reiterate that these techniques really work. Students of mathematics, computer science, and logic would all benefit from truly setting aside 25-minute intervals (with no phones, no laptops, etc.) to focus on some problems. Getting rid of all distractions gives your mind the time it needs to solve the problem; distractions make it so that your mental effort is diluted and this may result in not solving the problem. Again, it may seem like you're spending a lot of time on a problem, but if you're letting yourself be distracted, more and more of your mental energy is subtracted from the task and you may never reach peak focus.

In chapter 7 of How We Learn, Dehaene (2020) reminds us that the ability to focus is one of the hallmarks of animal intelligence, human or otherwise. Interestingly, our ability to focus has some drawbacks. In particular, when you focus on something, you lose focus of all else. Inattentional blindness is example of this. Check out the following video:

 

 

Dehaene also discusses the myth of multitasking. In multiple experiments, subjects demonstrate a significant delay in processing information when they are “multi-tasking.” However, because subjects cannot assess how rapidly they are performing a task until they’ve switched their attention to that task, subjects are unaware of the delay in processing. And so, subjects often believe there is no delay in processing, even though objectively there is. Dehaene adds that perhaps one can multitask if they undergo intensive training in one of the tasks, but this is very rare. In short, you can't multitask while learning logic.

I might add that if you haven't memorized the rules of inference, you should focus on that first. Chunking will be necessary for natural deduction to actually be natural. You need to know those rules well. Practice writing them out without looking at them. Do this multiple times a day. Re-write those that you got wrong several times correctly. Eventually, you have to just be able to intuitively recognize these patterns. If you don't, you will only become frustrated as you try to continue with the lessons. More importantly, you cannot be successful in this class without having mastered the inference rules—plain and simple.

But I don't want to close this section on a negative note. So let me mention this. Chunking is a powerful technique. Hofstadter (1999, ch. 12) reminds us that chunking is precisely what chess grandmasters do, which explains why they are able to memorize hundreds of games. If you teach yourself this technique, you can apply it to the rest of your studies. This might be the difference between a successful journey through academia and a not so successful one. Remember: train smart, not hard.

Getting started (Pt. II)

 

 

FYI

Homework— The Logic Book (6e), Chapter 5

• Re-do problems in 5.1.2E (p. 166).

• Re-read p. 167-173.

• Do problems in 5.1.3E (p. 173-174).

• Read p. 174-209.

• Do problems in 5.3E #1, a-i (p. 209).

• By the way, here is the student solutions manual.

 

Footnotes

1. Lewis Carroll, born Charles Lutwidge Dodgson, was not only a talented writer in the genre of so-called literary nonsense; he was also a logician and mathematician.