Introduction to Course

 

 

 

Beginnings...

Students hardly know what to expect when they begin this course. It's completely understandable. Formal languages are hardly ever taught as formal languages. In other words, up until now, you've probably never been explicitly taught a formal language. But that is precisely what will happen in this course.

What is a formal language?

A formal language differs from a natural language in that natural languages tend to be much more fluid and, in a way, ambiguous. I sometimes marvel about how the phrase "Not bad" can be interpreted in multiple ways. If someone says this to you after you asked them how a movie is, then you can interpret them as saying, "The movie is good." If, however, you are debating how good a movie is, someone might say this phrase emphasizing the second half: "It's not bad." Now they're suggesting that, sure, maybe it's predictable or maybe it's slow in the beginning, but overall it's not (that) bad of a movie. And sometimes(!), if you say "Not bad" with a certain wink in the eye, you don't just mean that it's good; you imply that it's really good. A person who is attempting to learn American English as a second-language would be forgiven if they can't quite grasp the meaning of the common expression "Not bad".

Natural languages also have funny syntax. Notice in the paragraph above that I included an exclamation point in parentheses in the middle of a sentence. This was placed there to emphasize that this is surprising. Notice that as you read it, you weren't confused about the overall meaning. You might've been slightly puzzled, but you didn't lose track of what was going on. I also inconsistently placed the period at the end of a quote: sometimes I put the period within the quotes and sometimes outside. But were you confused at any point? Probably not.

Formal languages lack these traits. For every string and operator in a formal language, terms which will be defined later, there is one and only one predetermined meaning. Moreover, if you violate a rule of grammar, like I did with the periods and quotation marks, then suddenly the expression is incoherent. Formal languages are far more strict than natural language. Unnaturally strict, in fact. It will be difficult to learn, but you'll gain insight into the way that many disciplines and technologies of the 21^st century work; you'll learn the type of language that they use.

Technically, you've already learned a formal language, although they likely didn't emphasize the formal aspect of it. However, as you were acquiring your mathematical knowledge, you were learning that certain operators work in certain ways and not in others; for example, the symbol "+" is for adding. You also learned that there are rules of grammar or "syntax rules" in mathematics. You know intuitively that the expression "4 ÷⁼", perhaps read as "Four divided to the power of equal sign"(?), makes absolutely no sense.¹

In this class, you'll be explicitly learning a formal language. In a nutshell, this was a language that was developed to answer the following question: If I know these things, do I also know this? Of course, you might want a more technical definition of logic. Let me try that now.

 

 

What is logic?

According to Herrick (2013), logic is the systematic study of the standards of correct reasoning; i.e., it is the study of the principles our reasoning should follow (p. 3). According to Hurley (1985), logic may be defined as the science that evaluates arguments; i.e., to develop a system of methods and principles that we may use as criteria for evaluating the arguments of others and as guides in constructing arguments of our own (p. 1). According to Bergmann, Moor, and Nelson (2013), what logic really does, in other words the hallmark of deductive logic, is truth-preservation. Reasoning that is acceptable by the standards of deductive logic is always truth-preserving; that is, it never takes one from truths to falsehood. Reasoning that is truth-preserving is said to be valid (p. 1-2).

As if the preceding weren't complicated enough, these writers are focusing primarily on one type of logic: first-order logic. There are actually various other types of logic, but we won't be going into those. We'll only focus on first-order logic, and so I'll drop the "first-order" and just say "logic."

At this point, you might be getting a little nervous. Don't worry. I've paced this class so that it is doable if you put in the work. In other words, it is a challenging class, but if you do all the assignments diligently at the time that they are assigned, you'll be fine. In fact, many students are impressed with themselves at the end of the course. If all goes according to plan, you should be able to read the deduction below.

 

 

 

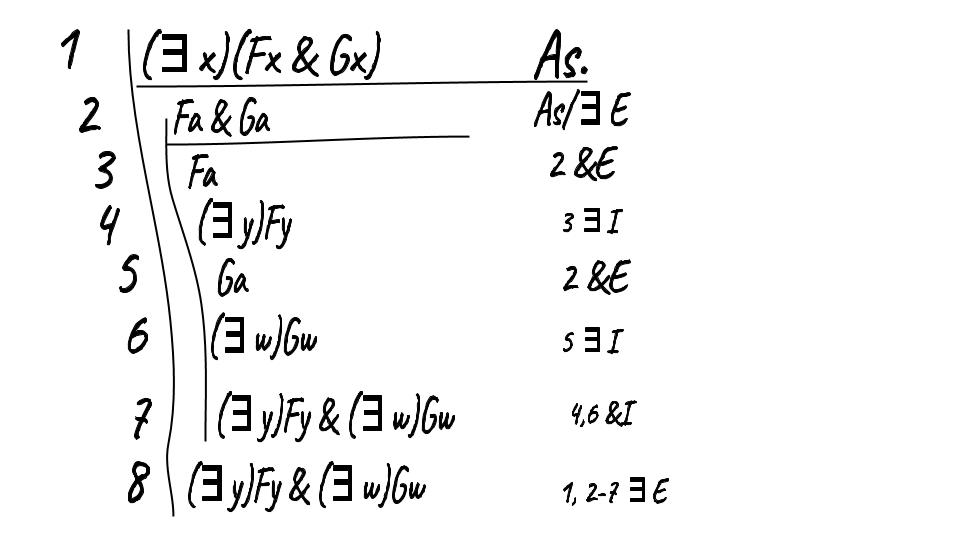
Important Concepts

Take a moment to go through the slides below. Make sure to memorize the important concepts of every lesson. It is on these concepts that the next lesson will build. Then the concepts from tomorrow will be the foundation for the concepts after that. Do not fall behind!

Also, although certain concepts won't make total sense right now, it's important to read the language used here to start to give your mind the tools it needs for understanding these concepts later. In chapter 1 of A Mind for Numbers, Barbara Oakley describes this activity as giving yourself "mental hooks" on which to hang tough concepts later. You'll be introduced to these tough concepts more formally later, when you are doing more focused thinking and learning.

Some comments

Logical consistency will be a cornerstone of everything we will be doing. We will define important concepts in this course, such as the notion of validity, in terms of logical cosistency, so it is important that you understand it. Logical consistency only means that it's possible that all the sentences in a set are true at the same time. That's it. Don't equate consistency with truth. Two statements can be consistent while being false. For example, here are two sentences.

• "The present King of France is bald."
• "Baldness is inherited from your mother's side of the family."

"The present King of France is bald" is false. This is because there is no king of France. Nonetheless, these sentences are logically consistent. They can both be true at the same time, it just happens that they're not both true.²

Arguments will also be central to this class. Arguments in this class, however, will not be heated exchanges like the kind that couples have in the middle of an IKEA showroom. For logicians, arguments are just piles of sentences that are meant to support another sentence, i.e., the conclusion. The language of arguments has been co-opted into other disciplines, such as computer science, as we shall soon see.

As you learned in the Important Concepts there are two major divisions to logic: the formal and informal branches. We will be focusing on formal logic. There are other classes that focus more on the informal aspect of argumentation, such as PHIL 105: Critical Thinking and Discourse. Classes like PHIL 105 focus on the analysis of language and the critical evaluation of arguments in everyday (natural) languages. One aspect of these classes that students tend to enjoy is the study of informal fallacies. Again, we won't be studying these here, but here's one just for fun:

Food for Thought...

 

 

 

On the horizon

What's ahead? I like to take a historical perspective in all my classes. I also like take a decidedly interdisciplinary approach. I consider this the best way to understand how ideas progress, how some ideas are updated and improved upon and how others are discarded. In fact, students that have taken a course with me before would be forgiven for thinking that I like history or cognitive science more than philosophy.³

Nonetheless, we will take every opportunity to look at how logic relates to other disciplines, in particular mathematics, computer science, and artificial intelligence. We will also begin at the very origins of logic and tell its full story, sort of... The origins of logic are actually a complicated issue. One type of logic originated in India in the 6^th century BCE. This logic had discernible syntax rules and was used to answer questions about the physical universe and the nature of knowledge. In China also, beginning around the 5^th century BCE, a system of logic was devised. However, we won't be focusing on these.⁴

In the 5^th and 4^th centuries BCE, in Greece, something truly special was happening. This is one of the reasons why we'll be focusing on the logic that originated in Greece, although there are others (see footnote 4). Here a new way of thinking was being developed. A student was allowed to disagree with his teacher, to provide criticisms to their argument, and to develop their own theory. This is a middle way between dogmatic obedience and crude deprecation. It was this way of thinking, when institutionalized centuries later, that gave science the property of self-correction. Although a full analysis of what was going on during the "Greek miracle" is far beyond this course, I can tell you that this period is undoubtedly influential on the rest of human history (see Rovelli 2017, chapter 1; see also Lloyd 1999), as you'll come to see.

 

 

Footnotes

1. I might add that in France, due to the influence of one of the greatests mathematicians of the 20^th century David Hilbert, some educational psychologists pushed for teaching mathematics from formal rules first, as opposed to the more intuitive practical way of learning about numbers by counting objects, adding piles together, subtracting some from the pile, dividing up piles, etc. Thankfully, this episode is over (see Dehaene 1999: 140, 241-42).

2. Contrary to popular belief, apparently baldness is not all your mother's fault. In the very least, smoking and drinking have an effect.

3. Philosophers have criticized me for not being enough of a philosopher. What I really attempt to do is use the tools and findings of Cognitive Science (and other relevant disciplines) to try to solve philosophical problems. In a sense, I believe most philosophical problems are actually empirical problems that haven't been framed properly.

4. There are many reasons for focusing on the Western Tradition, and so I'd like to preempt any accusations that the college is being Eurocentric in requiring this particular class. It is true, of course, that Europeans and the descendants of Europeans had come to dominate much of the world by the middle of the 20^th century, whether it be culturally, economically, politically, or militarily (as in the numerous American occupations after World War II). It's also true that European standards (of reasoning, of measuring, of monetary value, etc.) have become predominant in the world as part of a general (if accidental) imperial project (see chapter 21 of Immerwahr's 2019 How to Hide an Empire). It's also the case that it is during this time period of European dominance during which public education was being formulated and put into practice, and so there is a tradition in universities of following this model and emphasizing the European role. In fact, some scholars (e.g., Loewen 2007, Aoki 2017) have hypothesized that the function of education is at least partially to indoctrinate students into the dominant culture, typically one endorsed by the elites. All of this is both true and irrelevant for why we are focusing on the Western tradition in this course. As it turns out, only Aristotle's logic focused on logical force. In Shenefelt and White's (2013) If A then B, the authors juxtapose Aristotle’s syllogistic and Indian and Chinese logic. Indian logic was apparently preoccupied with rhetorical force more than anything. It featured repetition and multiple examples of the same principle so that it's primary function was persuasion. Chinese logic apparently did study some fallacious reasoning, but (strangely) never its counterpart (i.e., validity). It was only Aristotle’s logic that focused on logical force, the study of validity itself. The Greeks wanted to know why an argument’s premises force the conclusion on you. In short, only Aristotle studies logical force unadulterated by rhetorical considerations, and this led to major historical events centuries (and millenia) later. The interested student should check out Shenefelt and White (2013), in particular chapters 1, 2, and 9.