Pascal's Wager
Essentially, all models are wrong, but some are useful.
~George E. P. Box
On the reluctance of using the Bible to defend one's belief in God's existence
When first encountering the philosophy of religion, many years ago now, I was surprised at how sophisticated theologians refrained from using the Bible in their argumentation. To my young mind, it was obvious that to argue for God's existence, the Bible is your most valuable tool. And yet, exactly the opposite strategy was in play, and it took me many years for me to discover why. I hope to now save you much of the trouble that I went through and summarize why recourse to the Bible is not a viable maneuver in defending belief in the existence of God.
The first reason for not utilizing the Bible to defend religious conviction has already been stated. Recall that Descartes and Locke noted that religious fanatics reasoned just fine, and were perfectly capable of coming to conclusions given some initial assumptions. The problem, they realized, was that religious fanatics held some radical religious assumptions—for example that Protestants were heretics who were poisoning minds and were leading souls straight to hell—without any proper justification for them (in Descartes' case) or that they simply could not be highly-confident about (as Locke argued). With regards to using the Bible to defend belief in God's existence, these beliefs are not independent of each other. Typically, either one believes both in God's existence and the truth of the Bible or in neither. In other words, one belief supports the other and vice versa. This is not bad in and of itself. However, the problem arises when one uses the first belief to support the second and then the second to support the first. This is circular reasoning, and it violates what we've been calling Aristotle's dictum.

The mental machinery behind this sort of circular reasoning is absolutely fascinating. In their recently revised Mistakes Were Made (But Not By Me), the authors explore the phenomenon of self-justification, our tendency to justify those beliefs and decisions in which we are heavily invested and/or cannot change easily. In other words, if we are heavily-invested and cannot change an action (like having lied in an interview to get a job) or a belief (like the belief that our career choice was the right one), then we are likely to engage in self-deception and claim that the choice/belief was the right one all along and that any reasonable person would've done or believed the same. Moreover, we are likely to selectively recall information that confirms the rightness of our action/choice and ignore threatening evidence—classic confirmation bias.
After explaining their theory, the authors go through many examples of self-justification in different professions and domains. Chapter 4—my favorite—details the phenomenon of false memories. They set up the topic by discussing various episodes in which false memories were implanted by well-intentioned therapists, including 'recovered' false memories of sexual molestation (where there never really was any abuse). The authors then discuss the real victims: those that were wrongfully convicted of the "crimes" in the recovered false memories. Most relevant to us, the authors stress that the therapists do not change their mind and do not question their techniques and clinical practices.
The general problem here is that the therapists' system of beliefs is a closed loop. If the patient gets better or recovers a memory, then the psychotherapist’s practice must’ve worked; if they didn’t get better or recover a memory, the patient must be resistant to therapy. In other words, there is no way to disconfirm the therapists' system of beliefs. It's not only clinical psychiatrists that are plagued by the curse of the closed loop. The authors provide details of closed loops in the criminal justice system (in the minds of both prosecutors and those that engage in interrogation), in politics, and even in romantic relationships. The same could be said about the closed loop of believing God exists because it's stated in the Bible, and believing that the Bible is true because it was inspired by God. It's a trap that's hard to get out of, since it requires admitting that we formed beliefs or took actions without good reasons (see Tavris and Aronson 2020).
One more thing that is relevant here is self-justification when choosing majors. In my own experience, I've met students who were originally in a major under the Behavioral and Social Sciences Division (where I am housed) who then switch to another division. Choosing a major is obviously a big decision; it can be nerve-racking and could define the course of the rest of your life. Because of this uncertainty, I've noticed the need for some students to make themselves more comfortable with their choice by ridiculing, attacking, or otherwise dissociating from their past major. However, it is perfectly possible to be, say, a math major without denigrating, say, psychology. The fact that these students felt compelled to disparage their former major, I think, is due to the mind's need for self-justification.

The second reason I'll give for why intellectuals from the past have repeatedly refrained from using the Bible to defend their religious convictions is that intellectuals tend to be committed to logical consistency and, unfortunately, the Bible has some glaring inconsistencies. If one engages in serious study of the Bible, one runs into problems early on. For example, the Book of Genesis has two incompatible creation stories. Why? Why would there be two stories of the origins of the world that are incompatible with each other right next to each other? Even more problematic is that the creation stories conflict with our scientific understanding of the world. For example, in the first creation story, God creates day and night before he created the sun (which is what determines when it is day and night). Obviously, the thinkers we've been covering were heavily invested in the science of astronomy of their day, and they would've recognized this little hiccup (in literally the first book of the Bible).
There are other problems. As we've seen before, the early Church had to deal with many (what would eventually be called) heretical versions of Christianity. We mentioned before the Arian heresy, which is the view that Jesus was not equal with God the Father but actually subordinate to Him. Reading the Bible closely, though, really does lead one to this sort of belief, a view sometimes called subordinationism. For example, if one looks at the Gospels, the genealogies of Jesus are very incriminating. If you have a Bible handy, take a look at Matthew's genealogy of Jesus, and compare it with that of Luke. Two things that are immediately obvious are this. First, they're not identical. Matthew's account is substantially shorter. Shouldn't there be agreement on this, though? Second, and perhaps more damning, is that the genealogies are patrilineal. In other words, they describe the male line of ancestry. They both end with Joseph and then Jesus. But, according to tradition, Joseph is the stepfather of Jesus; Jesus was born of Mary, who is said to have been a virgin all her life. And so, it doesn't make sense to give a patrilineal genealogy since Joseph is not the father. Subordinationists used this to argue that Jesus was actually just a human and, at least in one version of the view, was adopted by God (see Ehrman 2005 and Ehrman 2015).1

Augustine of Hippo
(354-430 CE).
One more issue with the Bible is not so much about the inconsistencies within but rather has to do with the quality of the writing. Apparently, the register (the level of formality of a piece of writing) and accent that the Bible was written in was “embarrassing” to many Christian intellectuals (see Nixey 2018, chapter 10). This, however, is difficult to understand for modern readers, since the process of translation has smoothed over some of the problems in the original Hebrew and Aramaic. One would have to both learn these languages and then find early copies of these texts to understand the complaint being given here. I, for one, don't speak either of these languages, so I can't make this claim directly. However, it is telling that some early Christian intellectuals did feel the need to defend the way the Bible was written. In fact, even Saint Augustine (354-430 CE), considered one of the most important Church Fathers of the Latin Church, felt the need to defend it (ibid., 160-61). The poor style of the biblical writers was even more obvious when compared to the superior pagan literature, including writings from non-Christian philosophers, medics, and even emperors.2
I'll give one more reason why the Bible is not often used by intellectuals to defend belief in God. This has to do with something that is taught in every class on public speaking or persuasive argumentation: know your audience. When one is defending religious convictions, it is typically against non-believers. Clearly, non-believers aren't going to be convinced by references to a book they don't believe is true. In short, no atheists are going to be convinced by a recourse to the Bible, so there's no sense in trying.
These are just some of the inconsistencies in and problems with the Bible; there are more. Rather than spending more time on this, though, I'll just say the following. If one is engaging in rational argumentation, books of supposed supernatural origin aren't going to have much explanatory power. Generally speaking, this strategy is a dead end.
And so, religious intellectuals from Anselm to Descartes have thought it best to steer clear of these biblical issues. Anselm and Descartes, instead of using the Bible in their argumentation, gave their different versions of an ontological argument. Aquinas and Paley argued from natural theology, as we've seen. The author we're covering today, though, went by an entirely different route.
“Let us now speak according to natural lights. If there is a God, he is infinitely incomprehensible, since, having neither parts, nor limits, He has no affinity to us [Ockham’s point]. We are therefore incapable of knowing either what He is, or if He is... Who then will blame Christians for not being able to give a reason for their belief, since they profess a religion for which they cannot give a reason?” (Blaise Pascal as quoted in Blackburn 1999: 186; interpolation is mine).


The human
Blaise Pascal was born in 1623. Due to his poor health, he did not enjoy regular schooling; rather, his father (who was an accomplished mathematician) taught Pascal a curriculum primarily consisting of classical languages and mathematics. He was never formally trained in theology or philosophy. At a very young age, he showed great promise for mathematics and, throughout his life, he met and corresponded with various influential mathematicians of the day, including some of the members of the Marsenne Circle, René Descartes, and Pierre Fermat.
When meeting with Descartes, Pascal likely told him about an experiment he would be conducting soon, the results of which were published in Pascal's Récit de la grande expérience de l'équilibre des liqueurs in 1648. With few exceptions, however, most of Pascal's works weren't published until after his death. This is because, throughout his life, his attentions oscillated between mathematics and his devotion to a very strict sect of Christianity started by Cornelius Jansen. In fact, Pascal's contributions to probability theory (likely what he is most known for besides the argument we'll be covering in this lesson) were not known until the Swiss mathematician Daniel Bernoulli used Pascal's insights in the early 1700s.
Towards the end of his life, he focused exclusively on a theological defense of Catholicism. He left bundles of notes to be published, but gave no directions on the order in which they should be organized. This posthumously published notebook is known as the Pensées, and it is from this body of work that we are pulling his argument for "wagering for God." In this passage, we can also see Pascal's early insights into probability theory.
““In another landmark moment in this passage, he next presents a formulation of expected utility theory. When gambling, ‘every player stakes a certainty to gain an uncertainty, and yet he stakes a finite certainty to gain a finite uncertainty, without transgressing against reason.’ How much, then, should a player be prepared to stake without transgressing against reason? Here is Pascal’s answer: ‘…the uncertainty of the gain is proportioned to the certainty of the stake according to the proportion of the chances of gain and loss…’ It takes some work to show that this yields expected utility theory’s answer exactly, but it is work well worth doing for its historical importance” ( Hájek 2018, Section 4).
Pascal's life was characterized by ill health and lifelong pain. Some commentators even speculate that he suffered from manic depression (see the Stanford Encyclopedia of Philosophy's Entry on Blaise Pascal). He died in Paris in 1662 at the age of 39.
Important Concepts
Decoding Pascal


Objections
The "mathematical error" objection
Many students are initially offput by the use of ∞ in Pascal's mathematical argumentation. But, this was a perfectly valid move in Pascal's time. The reality is that mathematical concepts have a messy history. Time and time again, new ideas and approaches to the study of mathematics were questioned, updated, debated, thrown out, and taken up again. For example, irrational numbers and non-Euclidean geometries were all looked upon suspiciously in the beginning. There's even a myth that some Pythagoreans, who believed that all numbers could be expressed as the ratio of integers, drowned the discoverer of irrational numbers (which can't be expressed as the ratio of integers). Similarly, in his survey of the cognitive science of mathematics, Dehaene reminds us that negative numbers were also heavily debated upon their introduction.
“For Pascal himself, the subtraction 0 - 4, whose result is negative, was pure nonsense”
(Dehaene 1999: 87).
This is, in fact, how real science is done. Real science involves debate, suspicion of another's findings, conflicting interpretations of data, and even challenging the experimental methodology of other scientists. It is far from a clean, heroic picture. Here are two examples of now-established scientific views which were initially looked at with wariness and one widely-held view that is now coming under attack:

- Einstein's relativity was not universally accepted at first. His views were confirmed (for most) only in 1919 when an eclipse afforded scientists the opportunity to see how a great mass can bend light (Kennefick 2019).
- Einstein himself could not accept quantum mechanics, always believing that there was a 'hidden variable' that would eventually be discovered and return something known as determinism to physics. (Stay tuned.)
- Today there's a debate in the neuroscience of emotion between those who believe that there are universally built-in emotions (the classical view) and the view that emotions are socially-constructed in different ways by different people (the construction theory of emotion; see Barrett 2017).
All this to say that Pascal likely had some good responses to this criticism, even if they are lost to history. All we can say is that it was perfectly acceptable for him to argue in the way he did given the state of mathematics at the time. It's unreasonable to accuse him of committing a mathematical error.3
The Many Gods Objection
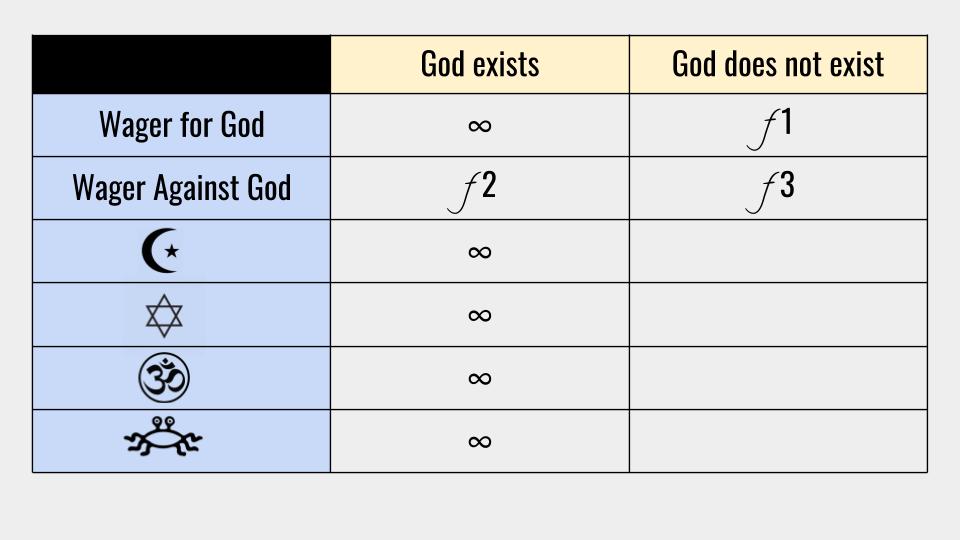
An extended decision matrix.
Another possible response to Pascal's wager comes from the admission that there are, in fact, many other competing religions. At least some of them are worthy of some probability in the decision matrix. However, the utility of some of these religions, such as Judaism and Islam, is also infinity. As such, if the probability that these religions are correct is non-zero, then these religions would also yield infinite expected utility. This would imply that there are multiple possible routes to infinite expected utility. Choosing Christianity, then, would seem like an arbitrary choice, and this is unjustified.
The Zero Probability Objection
Perhaps the most damning—no pun intended—objection to Pascal's wager is the zero probability objection. The atheist might argue against premise 2; i.e., she might claim that the probability of God existing is actually zero. Perhaps this atheist is assuming that the problem of evil is valid and sound. Since the conclusion of the problem of evil argument states that the very concept of God is incompatible with the world as we know it, it entails assigning a probability of zero to God's existence. In this case, the expected utility is 0, (since ∞ X 0 = 0). If this atheist is correct, it makes no sense to wager for God, since you're better off choosing another row in the decision matrix where there is at least the chance of an expected utility that's greater than zero. A lot rides on whether or not the problem of evil can be solved...



The thinkers from the early modern period who held religious convictions typically did not recourse to the Bible to defend their faith; they used rational argumentation instead.
Blaise Pascal gives an argument suggesting that believing in God might be rational despite the absence of a convincing argument for God's existence.
Pascal's argument, however, might be problematized by arguments like the Problem of Evil, which one can interpret as arguing that there is zero chance that God exists.
FYI
Suggested Reading: Alan Hájek, Pascal’s Wager (Note: Focus primarily on sections 1, 4, & 5.)
TL;DR: Crash Course, Indiana Jones and Pascal’s Wager
Related Material—
- Video: TED, Dan Gilbert: Why We Make Bad Decisions
- Podcast: Making Sense Podcast, What is and what matters: A Conversation with Rebecca Goldstein and Max Tegmark
- Note: In this recording of a live event, Sam Harris and his guests Rebecca Goldstein (a philosopher) and Max Tegmark (a physicist) discuss how, in effect, it seems like science has a little philosophy built into it. This is because the interpretation of empirical data is theory-laden. Put into the language that we've been using, although scientists in a given field are all looking (roughly) at the same data, their interpretations sometimes differ. That is, scientists import a little bit of their worldview into their work. They interpret data using the assumptions of their worldview.
Advanced Material—
-
Note: In this lecture, we utilize decision theory to assess Pascal's argument. Here is an introduction to decision theory.
-
Reading: Katie Steele and H. Orri Stefánsson, Stanford Encyclopedia of Philosophy Entry on Decision Theory
Footnotes
1. Fun fact: A student once came up to me after this lesson and told me that a. she really enjoyed the lesson and was thinking a lot about the content, and b. she felt like just studying this was sinful and she felt the need to go to confession.
2. The fact that non-Christian literature appeared to many to be more sophisticated led to a process by which Christians began to Christianize and absorb the pagan literature, at least in part due to self-interest. Augustine is given credit for "christianizing" Plato. Aquinas "christianized" Aristotle.
3. Students, unfortunately, often come to higher education with overly-simplistic views of science where there are people in lab coats producing facts. Many have an even more simplistic view were scientific progress is basically the labor of just a handful of thinkers. Science—real science—is dynamic, combative, competitive, and this is actually what makes it so effective. It's history—it's real history—has tens of thousands of views that were discarded because they didn't work out. The fact is that science, generally speaking, progresses through hundreds of small discoveries, hundreds of labs working independently (and competitively), fighting for the same grants (their sources of funding), and it is only time that definitively weeds away the non-productive theories. Part of the reason why students have some of the more unsophisticated beliefs about science is because the history of science really is taught like its a heroic tale, where the good guys have the right idea, but some others were nay-sayers, but in the end the good guys always win. Essentially, I'm blaming K-12 education. Again, the reality is much more convoluted than this. For example, in chapter 11 of his Not Even Wrong, Woit argues that most histories of physics and mathematics of the 20th century—like his own—ruthlessly suppress and ignore research programmes that ultimately failed, making it seem like most researchers were working on the theories that ultimately prevailed. However, Woit makes clear that the reality was that a majority of physicists weren’t working in the “triumphant” research programmes; only a minority of thinkers were working on the projects that were actually successful. Let me say that in a different way to drive the point home. Most physicists working on particle physics in the time period Woit describes were wrong. They worked on theories that ultimately failed. Now this is (to me) heroic in its own way; but this is not the tale of science that our educational system imparts on our students. They want to tell a neat tale of success, and this (unfortunately) obscures reality.
One last point that seems relevant here. We're beginning to see something peculiar. Time and time again, some intellectual insight is preceded by some mathematical breakthrough. Consider the relationship between mathematics and physics. Time and time again, mathematicians have created tools that would eventually become useful to physicists even though mathematicians never intended to be that way. Non-Euclidean geometry, for example, pre-dated relativity theory; representation theory was eventually used in Schrödinger’s equation; and Clifford algebra was used in Dirac’s equation (which is basically Schrödinger’s equation but also is compatible with relativity theory). This is strange. It's almost as if the world necessarily conforms to mathematical law, and so mathematicians, by simply engaging in pure mathematics, develop tools that will eventually be useful in understanding the world (even though this was not their intention). Is mathematics the key to understanding reality? And if it is, why is this the case? Stay tuned.

