Quantifier Rules
(Pt. I)

Making Progress
At the beginning of Unit IV, we laid out some queries that still needed to be addressed. We have dealt with two of those. One, we know that Stoic truth-functional logic is the first version of primary logic even though it was Aristotle who first initiated the study of validity. Two, we also know that Stoic valid argument forms do grasp at an underlying logical form that is always valid.
We can ponder a bit about this second point. Why is it that logical truths are true? What makes logical truths, like mathematical truths, be (or appear to be) necessary? Some people have thought that it is simply a function of our language. Although this predates the 20th century, one very famous philosopher named Ludwig Wittgenstein argued forcefully for this thesis, claiming that logical truths are only true because they are true by definition. This, in effect, makes logical truth a consequence of our language.
But a moment's reflection tells you that this can't be. This is because linguists have come to learn that our language already follows an internal logic. In other words, languages—whether we recognize it or not—appear to have a rule-driven organizing scheme to them. In short, logic is what makes our language possible and not the other way around (see Shenefelt and White 2013: 65-70).

The inquiry into why logico-mathematical truths seem to be necessary and timeless have driven some to believe that there is an underlying logico-mathematical reality that is more fundamental than the physical reality that we see. Famously, Plato believed that the study of mathematics is a pathway to understanding the true nature of reality. Recently, relatively speaking, even Darwinian processes—which are instantiated in physical, living organisms—have been explained in purely (non-physical) mathematical terms (see Smith 1982). More ambitiously, physicist Max Tegmark (2015) argues that reality itself is a mathematical construct, and cognitive scientist Donald Hoffman, in his own way, argues that mathematics has a primacy over physical reality. Is reality based on a logico-mathematical foundation? How would we know?
These questions are far beyond this course, obviously; and they are perhaps even past the realm of what can be known by humans. We can only hope to make slow, steady progress in our own limited understanding.
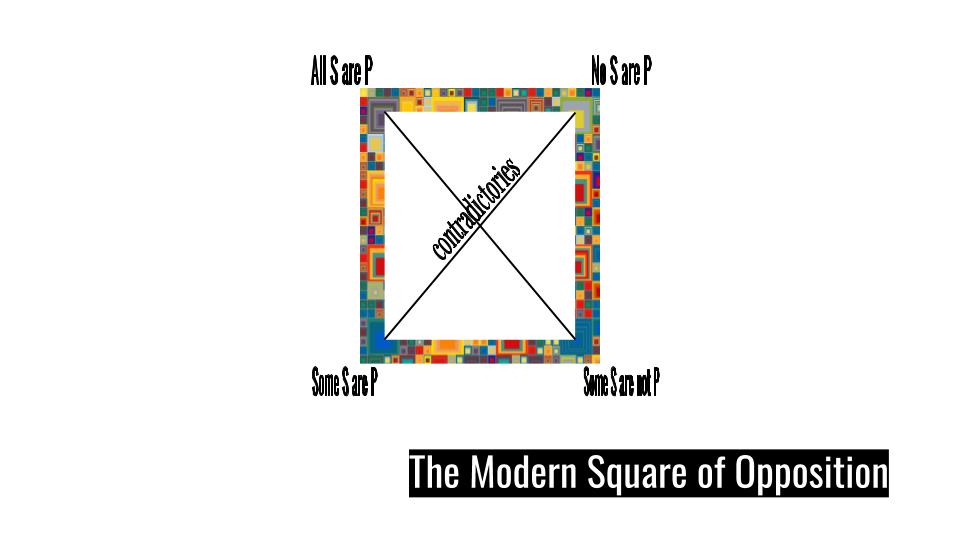
One thing we can solve at this moment is the puzzle of logical relativity. Recall that some arguments were valid depending on whether one took the hypothetical viewpoint or the Aristotelian existential viewpoint. Recall also that, when we posed this puzzle, we still had no way of expressing this distinction in our symbols. But now we do: "(∀x)" and "(∃x)".
Note that if we want to represent the existential viewpoint, we simply need to use the existential quantifier. Note also that if we make a universal claim, like "All F are G", we use a conditional: (∀x)(Fx ⊃ Gx). This, of course, is the hypothetical viewpoint: if F's exist, then they are G. And thus, we can represent both viewpoints in our symbolizations. The puzzle of logical relativity is solved.


Important Concepts
Clarifications
Universal elimination (∀E)

∀E is a very intuitive and easy to use rule. The general notion is that you can move from a universally quantified sentence to a sentence where the universal quantifier is removed and the variable(s) that the quantifier was ranging over is/are replaced with individual constant(s) (a-v). For example, we can legally move from "(∀x)(Px)" to "Pa". This is because the first sentence states that the property P is true of everything. That's why the universal quantifier is used. It literally says, "For all x, x has the property P." And so, if everything in the universe of discourse has the property "P", certainly the individual constant "a" has this property. And so we can legally infer "Pa".
Here are some other examples:
"(∀y)(Hy ∨ Ty)" → "Hb ∨ Tb"
"(∀w)(Rww)" → "Rcc"
"(∀z)(Mz & Nz)" → "Md & Nd"
Existential introduction (∃I)

∃I is also fairly intuitive and easy to use. An ∃I occurs when you move from a predicate letter paired with one (or more) individual constants to that same predicate letter now paired with one (or more) variables and a matching existential quantifier. The basic intuition is that if you know that some individual constant has some property, then you know that something has that property. For example, if you know "Socrates is a philosopher", then you know "Someone is a philosopher". You are basically abstracting away from a more descriptive statement containing an individual term to a more general statement utilizing an individual variable.
Here are examples:
"Ra ⊃ Qa" → "(∃x)(Rx ⊃ Qx)"
"Kss" → "(∃y)(Kyy)"
"(Lu & Mu) & Ou" → "(∃w)((Lw & Mw) & Ow)"
Universal introduction (∀I)

∀I allows you to move from a predicate letter paired with one (or more) individual constants to that same predicate letter now paired with one (or more) variables and a matching universal quantifier. This move is legal to use as long as the transition meets the following qualifications:
- The individual constant you are replacing with a variable does not appear anywhere in the assumptions.
- The individual constant you are replacing with a variable does not appear in the sentence you performing ∀I on.
The general idea of the second point is that, if you get rid of some individual constant, you have to get rid of it in the entire sentence. For example, you can't move from "Faa" to "(∀x)(Fxa)". Clearly "a" appears in the sentence you are doing an ∀I on, and that's not allowed.
I suggest that you read p. 474-490 of Chapter 7 of The Logic Book for more explanations, analysis, and examples. The link is in the FYI section below.
Existential elimination (∃E)

∃E is a subderivational rule. In fact, it is the most powerful subderivational rule. The setup, however, is a little tricky. You have to begin, obviously, with an existentially quantified sentence (much like how ∨E has to begin with a disjunction). Then you make a subderivation with the assumption being an instance of the existentially quantified sentence. What this means is that you have to replace the variable(s) in the existentially quantified sentence with an individual constant.
However, the constant that you use has to meet the following qualifications:
- The individual constant cannot appear anywhere in the assumptions of the derivation, i.e., the premises.
- The individual constant cannot appear anywhere in the existentially quantified sentence that you are basing your subderivation on.
- This is the existentially quantified sentence that you have to begin with. Sometimes this sentence appears in the premises and so this criterion is redundant. Nonetheless, it's important to check for this.
- The individual constant cannot be in the sentence you are trying to derive.
The power behind ∃E is that anything that you can derive in that subderivation you can place on the main scope. So, typically, if you use ∃E, your subderivation will get you your conclusion. Once you've arrived at your target sentence, you simply end the subderivation and then write the last line of your subderivation on the main scope, justifying it with the existentially quantified sentence you began with and the subderivation.
This is a tough one to understand, so I suggest you watch the portion of the video where I explain this a few times. Also, note that the name ∃E is a little deceptive. This is because what you end up with might still be an existentially quantified sentence. This makes it seem like you didn't eliminate anything. However, the elimination portion of the rule occurs when you move from the existentially quantified sentence you are beginning with to the assumption for the subderivation. That's why it's called existential elimination.
Again, I insist that you take a look at the readings for this lesson for more clarifications.
Getting Started (Pt. IV)
Tablet Time!

FYI
Homework— The Logic Book (6e), Chapter 10
- Read p. 474-490.
- Do 10.1E #1-2, p. 490-1.
- Here is the portion of the student solutions manual for the relevant chapter.

