The Square of Opposition

 

 

Level I: Immediate Inferences

So far we've only assessed arguments using the Imagination Method, basically thinking through premises and intuiting if the conclusion necessarily follows. Such informal methods are helpful with simple arguments, but their usefulness would vanish in more complicated cases. More formal, rigorous methods had to be devised. We'll begin, as promised, with short one-premise arguments.¹

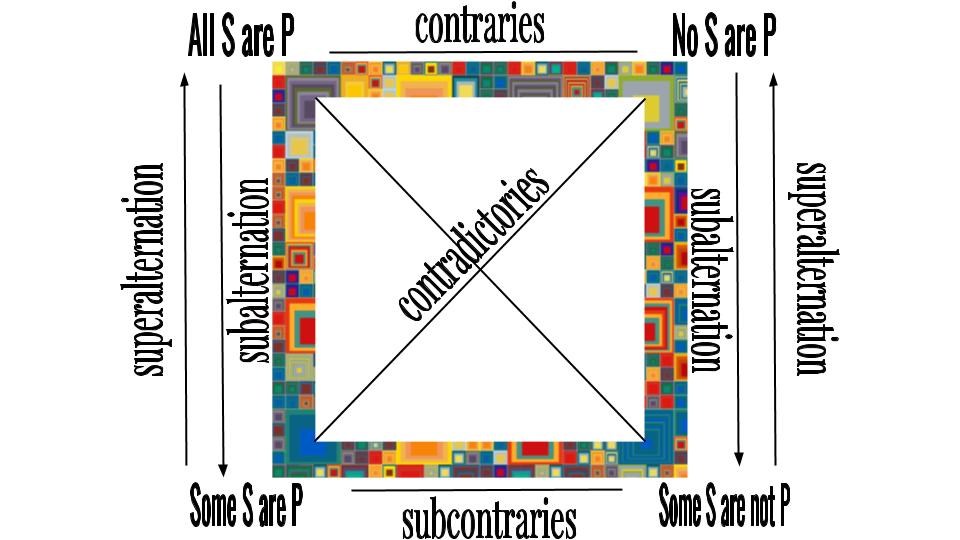
For reference, here are the steps for using the square of opposition.

1. Write out the argument.
2. Assess which type of sentence of categorical logic the statement is and write the letter beside the premise.
3. Write the truth-value (either T or F) next to the sentence letter of both the premise and the conclusion. (Note: If the sentence is just asserted, that means it’s true.)
4. Use the different logical relations in the square of opposition—such as superalternation, subalternation, etc.—to discover what the truth-value of the premise implies. In other words, Use the square of opposition to figure out the truth-value of the rest of the sentences given the premise. But remember(!), use ONLY the premise.
5. Check that the truth-value of the conclusion matches the truth-value for the relevant sentence-type on your square of opposition. If they do match, the argument is valid; if not, it is invalid.

 

 

FYI

Assessing Categorical Arguments for Validity: Immediate Inferences Edition

Directions: Use the Traditional Square of Opposition to check if the following one-premise arguments are valid or invalid.

Note: Some of these statements may first have to be put into standard form.

1. Some cookie-eaters are cookie monsters. So it is false, that no cookie-eaters are cookie monsters.
2. It is false that some cookies are turnips. So, no cookies are turnips.
3. It is false that some cookies are not delicious. So, it is false that no cookies are delicious.
4. It is false that all cookies are metallic. So, it is true that some cookies are metallic.
5. Some cookies are not splurps. So, no cookies are splurps.
6. Some cookie monsters are cookie lovers. So, all cookie monsters are cookie lovers.
7. It is false that no dogs are cookie eaters; hence, it is false that all dogs are cookie eaters.

 

 

 

Tablet Time!

 

 

 

Storytime!

 

In the late 18th century, the German philosopher Immanuel Kant wrote that logic “has not advanced a single step, and is to all appearances a closed and completed body of doctrine... There are but few sciences that can come into a permanent state, which admits of no further alteration. To these belong logic and metaphysics” (Kant as quoted in Haack 1996: 27). We can say definitively that Kant was wrong. He was about as wrong as you could be on this topic. Not only were there improvements to the logic of his time, various other "logics" sprouted and whole new disciplines arose which had at their foundation a form of logical analysis.

Although I'm not always terribly forgiving of Kant's views, in this case, I might be more lenient. From Kant's vantage point, it really might've looked as if logic was "closed and complete", at least in the West. In Susanne Bobzien's Stanford Encyclopedia of Philosophy Entry on Ancient Logic, she writes that Aristotle's logic "was taught by and large without rival from the 4^th to the 19^th centuries CE" (see the section on Aristotle for quote). This is surprising because, in Aristotle's time, there existed rival forms of logical analysis. We will meet the main challenger in the next unit. A question naturally arises. How did Aristotle come to dominate?

The more one studies history, the more one realizes that ideas don't always win out because they are better. Sometimes they get a little help. And other times it's just luck. In the case of Aristotle and his logic, it's a little bit of both. The story is complicated, but here's what we can say. Nearly all of the writings of the Stoics, the founders of the school of logic that was the main competitor to that of Aristotle, are lost. How they came to be lost is why this story is so complicated. I can't tell the full story here, but at least part of it is due to the rise of Christianity and the cleansing of pagan and heterodox literature. The interested student can read Freeman's (2007) The Closing of the Western Mind: The rise of faith and the fall of reason and Nixey's (2018) The Darkening Age: The Christian Destruction of the Classical World.²

In any case, Aristotle did dominate, basically unquestioned. That is until George Boole (1815-1864) publishes The Mathematical Analysis of Logic in 1847. Boole was a mathematician that spent his brief career at Queen's College, Cork in Ireland where he has a monument (pictured above). To try to explain Boole's contributions to the modern world this early in the course will be futile. We will revisit his ideas later on in more detail. For now, we will say only two things. First, most historians of computer science agree that Boole laid down the foundations for the information age. Second, and more related to our current task, Boole made the first improvement to Aristotle's logic in over a millennium.

 

 

Hypothetically...

Consider the following proposition: “All dragons are things that are magical.”

You don't really want to say that it's true, do you? Wouldn't that imply that you think dragons are real? But you don't want to say it's false either. You want to say both that dragons are imaginary creatures and that, in the traditional conception of these imaginary creatures, magic is involved. There! We said it. Easy enough. But how would we represent this categorical logic?

Imagine someone asserts the sentence "All of Roberto Bolaño's books are at least 200 pages" (see image above). Put into standard form, "All books written by Roberto Bolaño are books with more than 200 pages" is an A-type sentence. As we learned in the previous section, a true A-type sentence implies a true I-type sentence. This would be that if "All books written by Roberto Bolaño are books with more than 200 pages" is true, then "Some books written by Roberto Bolaño are books with more than 200 pages" is also true. That's basic subalternation.

This is where the trouble begins. Imagine someone asserts the sentence “All dragons are things that are magical” or "All harks are things that are very scary". Harks are indeed scary, by the way (click here). However, to say "All harks are things that are very scary" is to imply "Some harks are things that are very scary"; and remember: to logicians "some" means "at least one". So, if you say "All harks are things that are very scary" is true, you necessarily are committing to the existence of harks. Harks, though, obviously don't exist. But when we say "All harks are things that are very scary", it's pretty clear what we're trying to get at. If harks existed, then they would be very scary indeed.

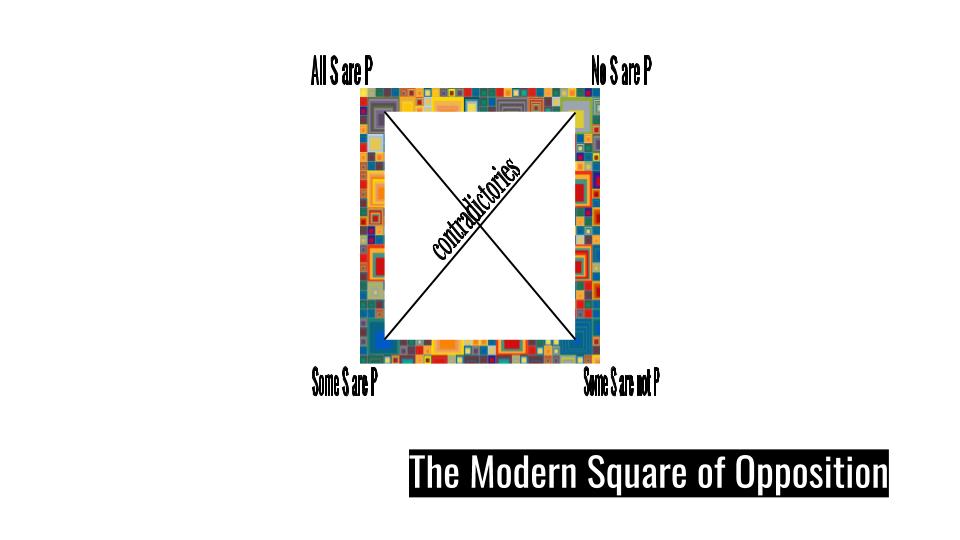
So what George Boole did is stipulated that you can take either the existential viewpoint or the hypothetical viewpoint. If you are talking about things that don't exist, you simply take the hypothetical viewpoint: If F's exist, then they are G. Although this seems like a simple enough fix, there is an unexpected consequence. The Square of Opposition is gutted. Many of its connections are lost. And so we are left with the traditional Square of Opposition if we are taking the existential viewpoint, and the modern Square of Opposition when we are taking the hypothetical viewpoint (pictured below).

 

 

 

Important Concepts

 

Next time...

Be sure to complete the homework for this lesson diligently. Catch-up on any lessons you haven't covered. Review if necessary. Drink lots of coffee. Do whatever you need to do to get ready for the toughest part of this unit...

 

 

FYI

Homework!

• Assessing Categorical Arguments for Validity: Immediate Inferences Edition Homework

 

Footnotes

1. On a technical/historical note, Aristotle himself didn't use the image of the Square of Opposition that we are using. Rather, this image was developed during the Roman imperial age using Aristotle's observations. But almost all of the relations were already present in Aristotle's work. In De Interpretatione, Aristotle discusses contraries and contradictories; in Topics, he discusses subalternation. Subcontraries were, however, an idea provided by later logicians. The Square of Opposition first appears in a commentary of Aristotle's De Interpretatione written by Apuleius of Madauros, written in the second century CE (Shenefelt and White 2013: 54n8).

2. I might add that this state of affairs was confined mostly to the West. As it turns out, other regions of the world were seeing a continued interest in mathematics, logic, philosophy, and the sciences, while Europe went into its Dark Age. For example, the Islamic empire grew so rapidly that they urgently needed administrators talented in mathematical and logical analysis to help hold the domains together. The Islamic rulers gave energetic support to these studies. "Books were hunted far and wide, and gifted translators like Thabit ibn Qurra (836-901) were found and brought to work in Baghdad... So diligent were the Arabs in those enlightened times that we often know of Greek works only because an Arabic translation survives" (Gray 2003: 41).