Truth-Tables
(Pt. II)

 

 

Truth-table Solutions from Truth-Tables (Pt. I)

 

 

 

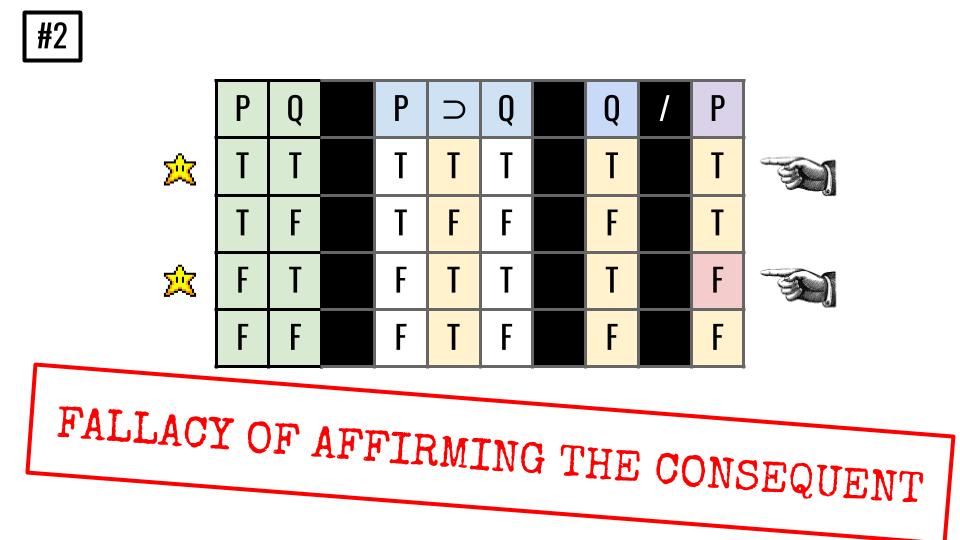
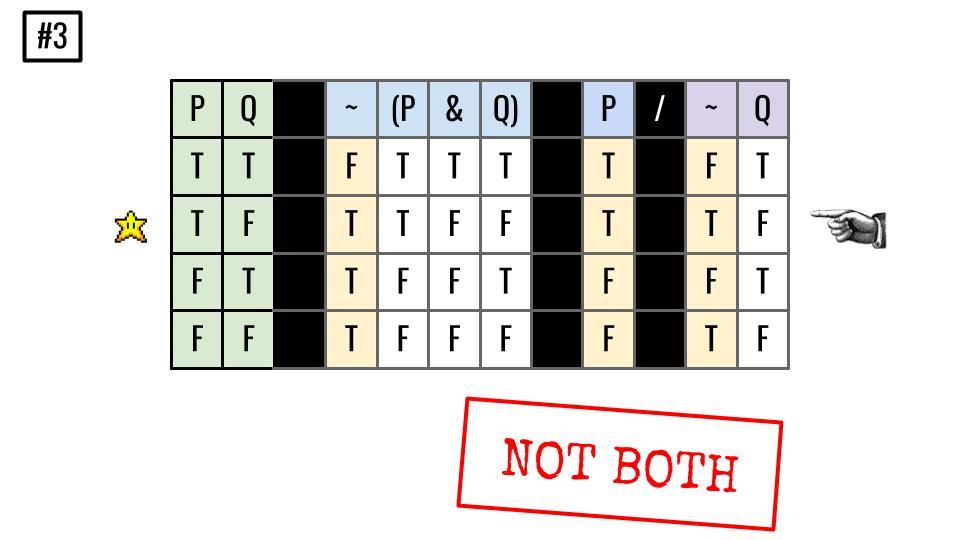
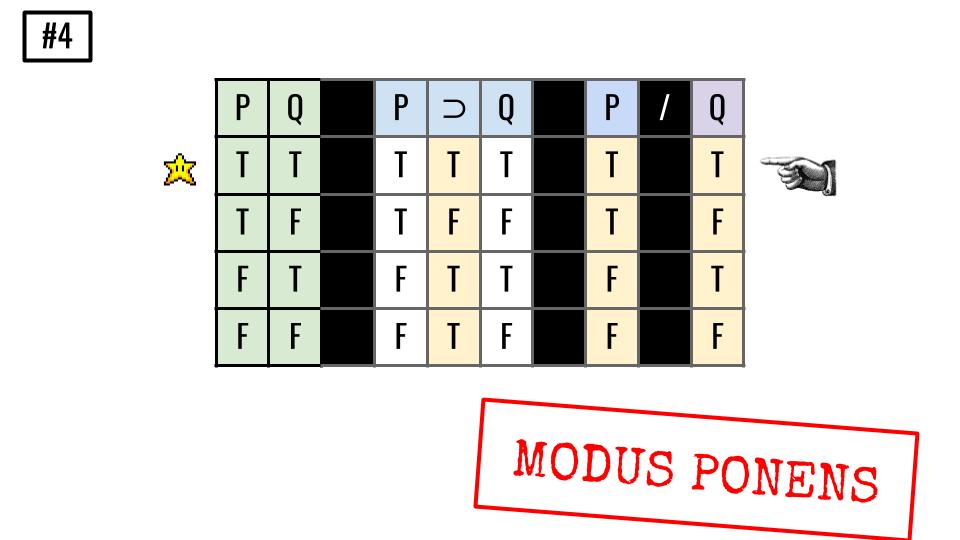
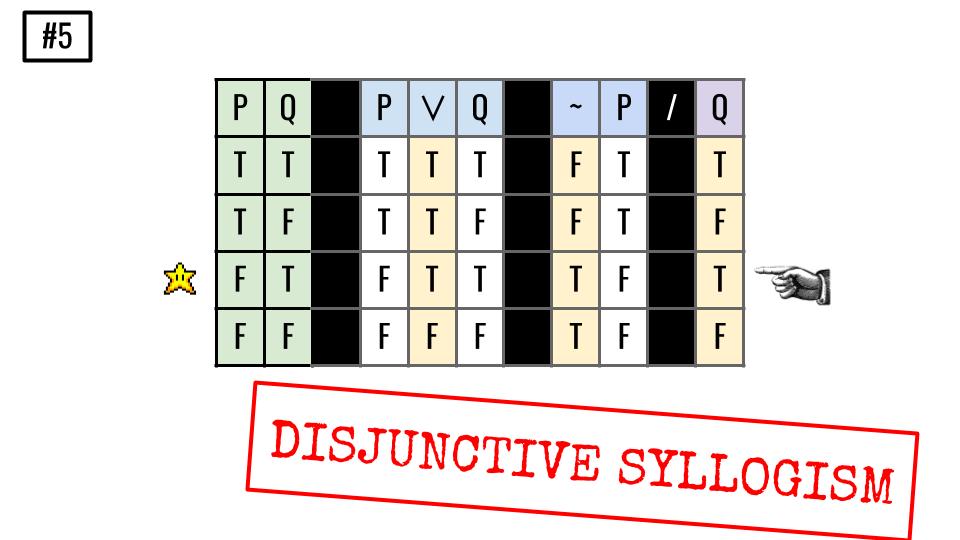
Important Concepts

 

Set Theory

At this point, we need to become comfortable with the language of set theory, or the mathematical theory of well-determined collections. We denote sets with curly brackets, "{" and "}". We refer to anything within a set as a member or element of the set. We typically use the capital Greek letter gamma "Γ" as a variable used to talk about sets of sentences of TL. A set with only one member is the unit set. And a truth-value assignment (or TVA) is an assignment of truth-values to the simple (or atomic) sentences of TL. These are actually the columns in our truth-tables that lay out all the possible truth-value combinations of the sentences of TL we are working with. In other words, the TVA is the columns in green from the previous section.

We also have to discuss the concept of isomorphism. The general idea behind isomorphism is that there is a mapping between two structures that can be inversed. They can be helpful in that, if you have two isomorphic objects, and if you understand one in a mathematically rigorous way, you can understand the other just as rigorously. For example, Douglas Hofstadter (1999: 53-60) reminds us that there is are some isomorphisms between mathematics and reality. There are countless examples where, if we understand the mathematics behind certain events in the real world, we can predict and control the actual events in the real world. In his 1999 book Gödel, Escher, Bach, Hofstadter speculates that as we discover the isomorphisms between mental processes and computer programs, we can begin to understand the mind better, since we have a firm understanding of computer programs (ibid., 568-73).

The reason why isomorphisms are important here is that we will now take our logical concepts of logical consistency, validity, logical truth, etc., previously expressed in the natural language of English, and we will express them in a mathematically rigorous way in the language of TL. Our formal language will shed greater light on our concepts expressed in natural language.

So, our concept of logical truth (which is that a sentence is logically true just in case it is not possible for it to be false) is isomorphic with the notion of truth-functional truth—a sentence of TL is truth-functionally true if and only if it is true on every truth-value assignment. Our concept of logical falsity (which is that a sentence is logically false just in case it is not possible for it to be true is isomoprhic with the notion of truth-functional falsity—a sentence of TL is truth-functionally false if and only if it is false on every truth-value assignment. Our concept of logical indeterminacy (which is that a sentence is logically indeterminate just in case it is neither logically true nor logically false) is isomorphic with truth-functional indeterminacy—a sentence of TL is truth-functionally indeterminate if and only if it is neither truth-functionally true nor truth-functionally false.

What does this mean for us in practical terms? It means that if the final column of a sentence of TL is all T's, then we know it is truth-functionally true. If the final column is all F's, then it's truth-functionally false. And if it has some T's and some F's, then it is truth-functionally indeterminate. This formal depiction allows us to understand more fully what is meant by the concepts of logical truth, logical falsity, and logical indeterminacy through the use of formal structures.

 

 

Food for thought...

Perhaps the most useful aspect of the isomorphism between logical concepts and their truth-functional expressions is that they really do illuminate what we mean when we use concepts like those implication, equivalence, and logical consistency. Consider the following statements:

In this set, A implies B; that is, if you know A, then you also know B. It is also intuitively obvious that they don't mean the same thing; i.e., they are not equivalent. Now consider the following set:

In this set, there is (intuitively at least) implication and equivalence. But can we express this intuitive notion formally?¹

 

 

 

Truth-functional equivalence and consistency

Here are some helpful rules:

• Rule for Equivalence Test: If two formulas on top of a table have matching final columns, then they are equivalent. If the final columns do not match, then the formulas are not equivalent.
• Rule for Consistency Test: Given two (or more) formulas side by side on top of a table, if there is at least one row where the main operator for all the formulas is true, then the sentences are consistent. If there is no row on which the main operators are true, the sentences are inconsistent.

 

 

Indirect truth-tables

 

 

FYI

Homework!

• This

Supplemental Material—

• Practice Problems: Merrie Bergmann, James H. Moor, Jack Nelson, and James Moor, The Logic Book, Chapter 3
  
  • Note: The interested student can find more problems for determining whether a sentence is truth-functionally true, truth-functionally false, or truth-functionally indeterminate in 3.2E #1 (p. 85), problems for determining whether a pair of sentences is truth-functionally equivalent in 3.3E #1 (p. 91), problems for determining whether sets of sentences are truth-functionally consistent or truth-functionally inconsistent in 3.4E #1 (p. 94), and problems for assessing the validity of an argument using truth-table analysis in 3.5E #1 (p. 102-103). Also, here is the student solutions manual for the chapter.

 

Footnotes

1. We will be covering the truth-functional concepts of equivalence and consistency, but will not be covering implication. To perform truth-table analysis in order to see if one sentence of TL P implies another sentence of TL Q, all one must do is draw a truth table for a conditional statement and place P in the antecedent position and Q in the consequent position. If the final column, that is the column of the horseshoe, reads all T's, then that is a valid implication; if not, then it is an invalid implication.