Universal Machines
It is possible to invent a single machine which can be used to compute any computable sequence.
~Alan Turing
Timeline I: The History of
Logic and Computation
Entscheidungsproblem
Our story begins in 1936, but, as you must've learned by now, all history is prologue. Choosing a starting point is arbitrary since everything that happens is influenced in some way by what happened before it. To understand what happened in 1936, you have to understand what happened at the turn of the 20th century.
In 1900, German mathematician David Hilbert presented a list of 23 unsolved problems in Mathematics at a conference of the International Congress of Mathematicians. Given how influential Hilbert was, mathematicians began their attempts at solving these problems. The problems ranged from relatively simple problems that mathematicians knew the answer to but that hadn't been formally proved all the way to vague and/or extremely challenging problems. Of note is Hilbert's second problem: the continuing puzzle over whether it could ever be proved that Mathematics as a whole is a logically consistent system. Hilbert believed the answer was yes, and that it could be proved through the building of a logical system, also known as a formal system. More specifically, Hilbert sought to give a finistic proof of the consistency of the axioms of arithmetic.1 His approach was known as logicism.
"Mathematical science is in my opinion an indivisible whole, an organism whose vitality is conditioned upon the connection of its parts. For with all the variety of mathematical knowledge, we are still clearly conscious of the similarity of the logical devices, the relationship of the ideas in mathematics as a whole and the numerous analogies in its different departments. We also notice that, the farther a mathematical theory is developed, the more harmoniously and uniformly does its construction proceed, and unsuspected relations are disclosed between hitherto separate branches of the science. So it happens that, with the extension of mathematics, its organic character is not lost but only manifests itself the more clearly" (from David Hilbert's address to the International Congress of Mathematicians).
As Hilbert was developing his formal systems to try to solve his second problem, he (along with fellow German mathematician Wilhelm Ackermann) proposed a new problem: the Entscheidungsproblem. This problem is simple enough to understand. It asks for an algorithm (i.e., a recipe) that takes as input a statement of a first-order logic (like the kind developed in PHIL 106 course) and answers "Yes" or "No" according to whether the statement is universally valid or not. In other words, the problem asks if there's a program that can tell you whether some argument (written in a formal logical language) is valid or not. Put another (more playful) way, it's asking for a program that can do your logic homework no matter what logic problem I assign you. This problem was posed in 1928. Alan Turing solved it in 1936.

Alan Turing.
Most important for our purposes (as well as for the history of computation) is not the answer to the problem, i.e., whether an algorithm of this sort is possible or not. Rather, what's important is how Turing solved this problem conceptually. Turing solved this problem with what we now call a Turing machine—a simple, abstract computational device intended to help investigate the extent and limitations of what can be computed. Put more simply, Turing developed a concept such that, for any problem that is computable, there exists a Turing machine. If it can be computed, then Turing has an imaginary mechanism that can do the job. Today, Turing machines are considered to be one of the foundational models of computability and (theoretical) computer science (see De Mol 2018; see also this helpful video for more information).
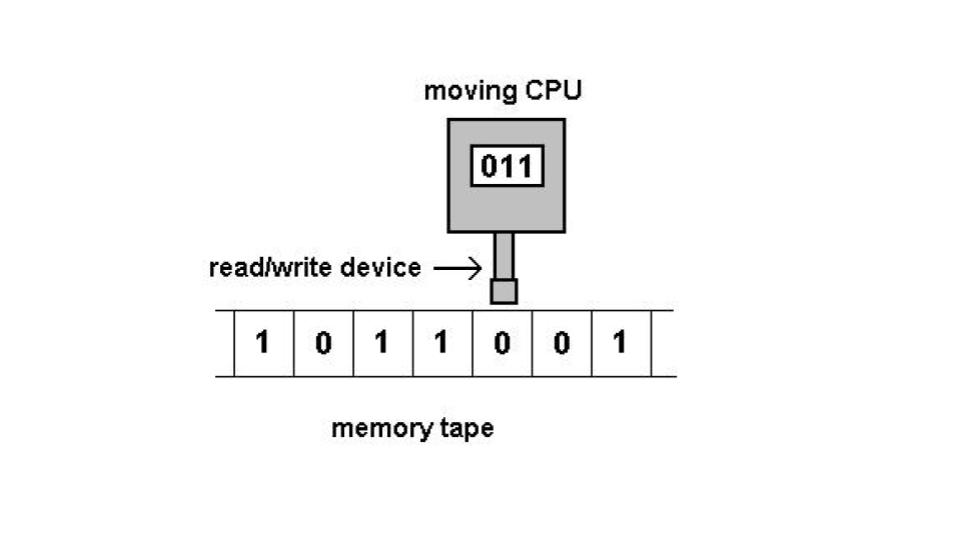
A representation of
a Turing machine.
What was the answer to Hilbert's second problem? Turing proved there cannot exist any algorithm that can solve the Entscheidungsproblem; hence, mathematics will always contain undecidable (as opposed to unknown) propositions.2 This is not to say that Hilbert's challenge was for nothing. It was the great mathematicians Hilbert, Frege, and Russell, and in particular Russell’s theory of types, who attempted to show that mathematics is consistent, that inspired Turing to study mathematics more seriously (see Hodges 2012, chapter 2). And if you value the digital age at all, you will value the work that led up to our present state.
Today, the conceptual descendants of Turing machines are alive and well in all sorts of disciplines, from computational linguistics to artificial intelligence. Shockingly relevant to all of us is that Turing machines can be built to perform basic linguistic tasks mechanically. In fact, the predictive text and spellcheck that are featured in your smart phones use this basic conceptual framework. Pictured below you can see transducers, also known as automatons, used in computational linguistics to, for example, check whether the words "cat" and "dog" are spelled correctly and are in either the singular or plural form. The second transducer explores the relationship between stem, adjective, and nominal forms in Italian.3 And if you study any computational discipline, or one that incorporates computational methods, you too will use Turing machines.
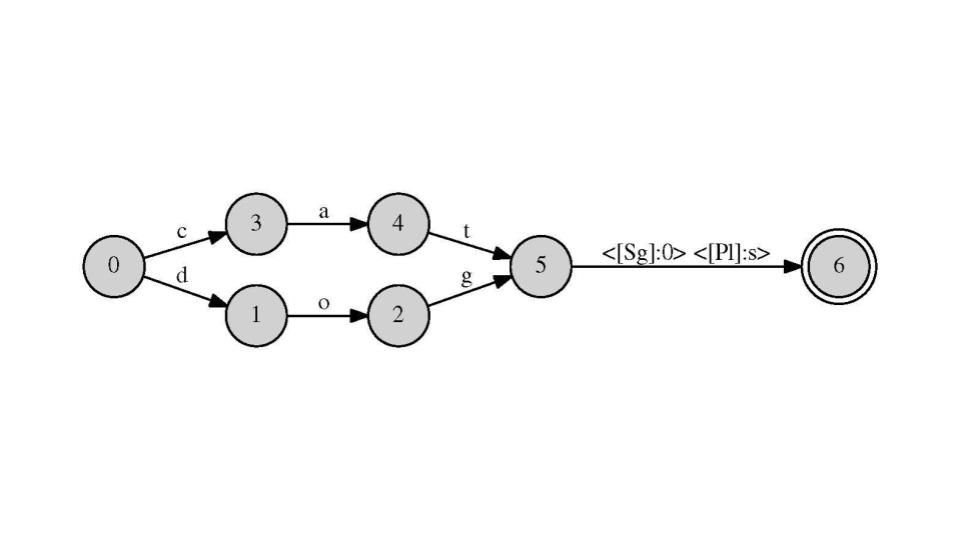
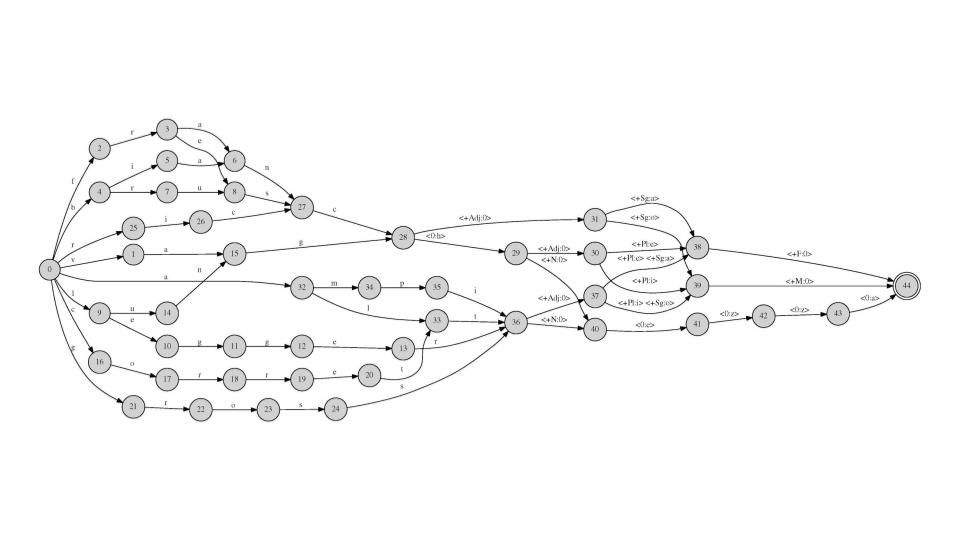

Timeline II:
Turing from 1936 to 1950
Important Concepts
Decoding Artificial Intelligence
###video goes here

Turing Test
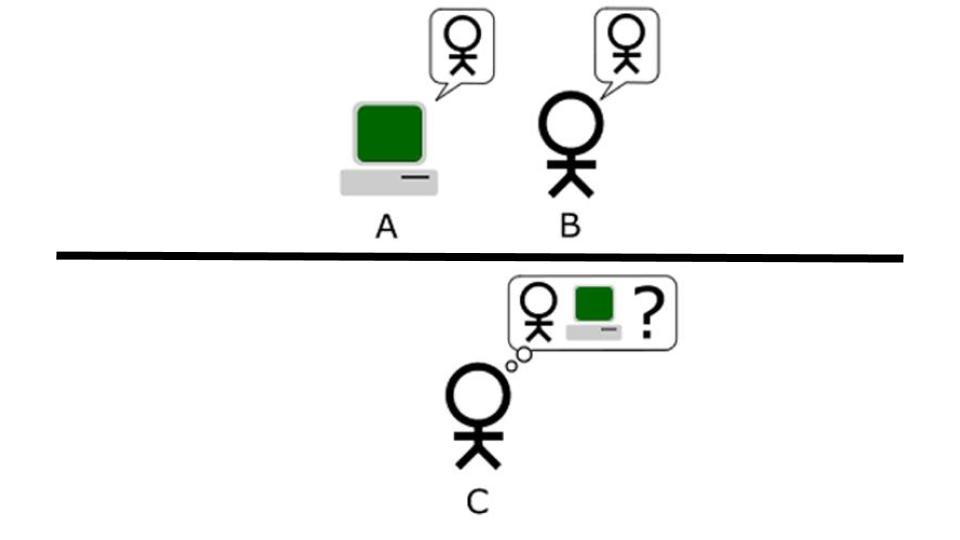
A Turing test.
With no conceptual impediment to stop machines from being intelligent, Turing began to dream up ways of testing machines for this most-human of traits. He was clearly influenced by the behaviorism of the age, as well as by some philosophical movements that were popular at the time. Most of the members of the Vienna Circle, for example, subscribed to the verification theory of meaning, which claimed that a statement is meaningful if and only if it can be proved true or false, at least in principle, by means of some sensory experience.4 And so, likely influenced by these trends in psychology and philosophy, Turing thought of a purely behavioral (and thus measurable) test for intelligence.
How will we know if a machine is intelligent? A Turing test is a test of a machine's ability to exhibit intelligent behavior equivalent to, or indistinguishable from, that of a human. It is modeled after the imitation game. In the imitation game, one man and one woman are in one room, while a judge is in a second room. The man and the woman are to pass notes to the judge without being seen or heard by the judge. The judge can ask questions of both the man and the woman, and they must respond. The man is supposed to be honest and try to help the judge figure out who the woman is and who the man is. The woman's role is to deceive. She must trick the judge into thinking that she's the man. If she can do this, she won the imitation game.
The Turing test is the machine version of this imitation game (see image). There is a judge who is communicating with both a human and a computer pretending to be a human. The human is supposed to be honest, saying things like, "I'm the human." The machine is lying. If the machine can trick the judge into thinking that it is human (at least a certain percentage of the time), then the machine passed the Turing Test. Here's a question for you to ponder: If not via the Turing Test, how would we know if a machine is intelligent or conscious? If you're stumped, then you've just come face-to-face with what's known as the problem of other minds: since consciousness can only be experienced from the first-person, you cannot know for certain that anyone else is conscious(!).

Decoding Turing
Timeline III: Turing's end
Artificial Intelligence today...
In a recent study, researchers presented machine learning experts with 70 occupations and asked them about the likelihood that they will be automated. The researchers then used a probability model to project how susceptible to automation an additional 632 jobs were. The result: it is technically feasible to do about 47% of jobs with machines (Frey & Osborne 2013).
The jobs at risk of robotization are both low-skill and high-skill jobs. On the low-skill end, it is possible to fully automate most of the tasks performed by truckers, cashiers, and line cooks. It is conceivable that the automation of other low-skill jobs, like those of security guards and parcel delivery workers, could be accelerated due to the global COVID-19 pandemic.
High-skill workers won't be getting off the hook either, though. Many of the tasks performed by a paralegal could be automated. The same could be said for accountants.
Are these jobs doomed? Hold on a second... The researchers behind another study disputed Frey and Osborne’s methodology, arguing that it’s not the entire job that will be automated but separate tasks within the job role more generally. After reassessing, their result was that only about 38% could be done by machines...
It gets worse...



In 1936, Alan Turing proposed an abstract computational mechanism in order to solve a problem proposed by the German mathematicians David Hilbert and Wilhelm Ackermann. We now know this as a Turing machine, and it is a foundational concept in theoretical computer science.
Soon after Turing's 1936 paper, he (and others) began to think that Turing machines might be useful models for how the mind works. Then, rapid progress in computer science prompted many to contemplate whether it was possible to build a computer capable of thought.
Seeing no viable theoretical objections to the possibility of machine capable of thought, Turing began to consider how to test for a machine's capacity to 'think'. Given the influence of behaviorism as well as that of a group of philosophers known as the Vienna Circle, Turing went with a purely behavioral test: check to see if a machine's behavior is indistinguishable from that of a human. We now call this the Turing test.
The field of artificial intelligence has taken off as of late and is showing signs that it might be both socially and economically disruptive.
Turing, despite being a war hero and computer science pioneer, was arrested for “gross indecency” (since acting on homosexual desires was illegal in the UK at the time) in 1952. To avoid imprisonment, Turing accepted probation along with a chemical castration (where anaphrodisiac drugs are injected so as to reduce libido and sexual activity). In 1954, Turing is found dead from apparent suicide.
FYI
Suggested Reading: Alan Turing, Computing Machinery and Intelligence
TL;DR: Crash Course, Artificial Intelligence and Personhood
Supplemental Material—
-
Video: TED-Ed, The Turing Test
-
Video: CrashCourse, Alan Turing
Advanced Material—
Reading: Michael Rescorla, Stanford Encyclopedia of Philosophy Entry on the Computational Theory of Mind
-
Reading: Graham Oppy & David Dowe, Stanford Encyclopedia of Philosophy Entry on the Turing Test
Footnotes
1. It was Kurt Gödel, whom we covered in the lesson titled 2 + 2 = 4(?), who dealt the deathblow to this goal of Hilbert. This was done through Gödel's incompleteness theorem in 1931. For more info, you can check out the Stanford Encyclopedia of Philosophy Entry on Gödel's incompleteness theorems or this helpful video.
2. Part of the inspiration for Turing's solution came from Gödel's incompleteness theorem (see Footnote 1).
3. Both transducers pictured were made by the instructor, R.C.M. García, using a program called Foma.
4. The view the Vienna Circle put forward was dubbed logical positivism. Among their tenets was a critique of metaphysics. Metaphysical statements are not empirically verifiable and are thus forbidden: they are meaningless. This is a result of their verification theory of meaning, which states that a statement is meaningful if and only if it can be proved true or false, at least in principle, by means of the experience. In other words, if a statement isn’t empirically verifiable (or a logical truth), then it is worse than false; it is meaningless. The only role of philosophy, according to most members of the Vienna Circle, is the clarification of the meaning of statements and their logical interrelationships via the building of linguistic frameworks, i.e., theories. For more information, see Karl Sigmund's (2017) Exact Thinking in Demented Times: The Vienna Circle and the Epic Quest for the Foundations of Science.

