Validity

Knowledge of the fact differs from knowledge of the reason for the fact.
~Aristotle
Origins...
Aristotle is the most famous student of Plato. He was prolific, writing on all major topics of inquiry established during the time that he was alive. Like his teacher, he also founded a school: the Lyceum. He was the tutor of Alexander the Great, son of Philip II. He was also the founder of the first school of Logic, a discipline he created and which is still studied when learning philosophy, computer science, and mathematics. You'll soon come to see why.1
"Aristotle was born in 384 BC, in the Greek colony and seaport of Stagirus, Macedonia. His father, who was court physician to the King of Macedonia [Amyntas III, father of Philip II], died when Aristotle was young, and the future founder of logic went to live with an uncle... When Aristotle was 17, he was sent to Athens to study at Plato’s Academy, the first university in Western history. Here, under the personal guidance of the great philosopher Plato (427-347 BC), the young Aristotle embarked on studies in every organized field of thought at the time, including mathematics, physics, cosmology, history, ethics, political theory, and musical theory... But Aristotle’s favorite subject in college was the field he eventually chose as his area of concentration: the subject the Greeks had only recently named philosophy… [And] Aristotle would write the very first history of philosophy, tracing the discipline back to its origins in another Greek colony, the bustling harbor town of Miletus... Thales of Miletus (625-546 BC) first rejected the customary Greek myths of Homer and Hesiod, with their exciting stories of gods, monsters, and heroes proposed as explanations of how the world and all that is in it came to be, and offered instead a radically new type of explanation of the world” (Herrick 2013: 8-9; interpolation is mine).
As you can see from the quote above (and as we mentioned last time), Aristotle was around during a time in which a new way of thinking was being devised. No, I'm not just talking about how this "super cool" new discipline of Philosophy was coming about. This so-called "Greek Miracle" is truly interdisciplinary and a historical landmark in intellectual history. Surprisingly, though, scholars have a hard time characterizing exactly what made this period so special. I'll give you two theories on this topic.
As we saw last time, some scholars stress the central role that debating took. Physicist Carlo Rovelli, when giving his history of quantum gravity, starts back in Ancient Greece, with the ideas of Democritus who, under the tutelage of Leucippus, develops atomic theory: things are composed of smaller objects which are indivisible.2 Rovelli stresses that students were allowed to debate their teachers, and that ideas had to be defended with more rigor. Historian of mathematics Luke Heaton agrees with Rovelli. Heaton notes the differences in the approaches taken by different cultures in the field of mathematics. For example, the ancient Egyptians performed calculations and inferences exactly in the ways of their ancestors. In fact, they literally believed this to be a matter of life and death. The whole cosmic harmony of their god Ma’at "could turn to chaos and violence if the ruler or his people did not adhere to their traditions and rituals." In other words, the Ancient Egyptians did things the way they had always been done, and could not even imagine of attempting new methods of mathematics. In contrast, however, Greeks debated mathematical truths. They emphasized the rigorous articulation of logical principles in argumentation (see Heaton 2017: 34-5; see p. 34 for quote).
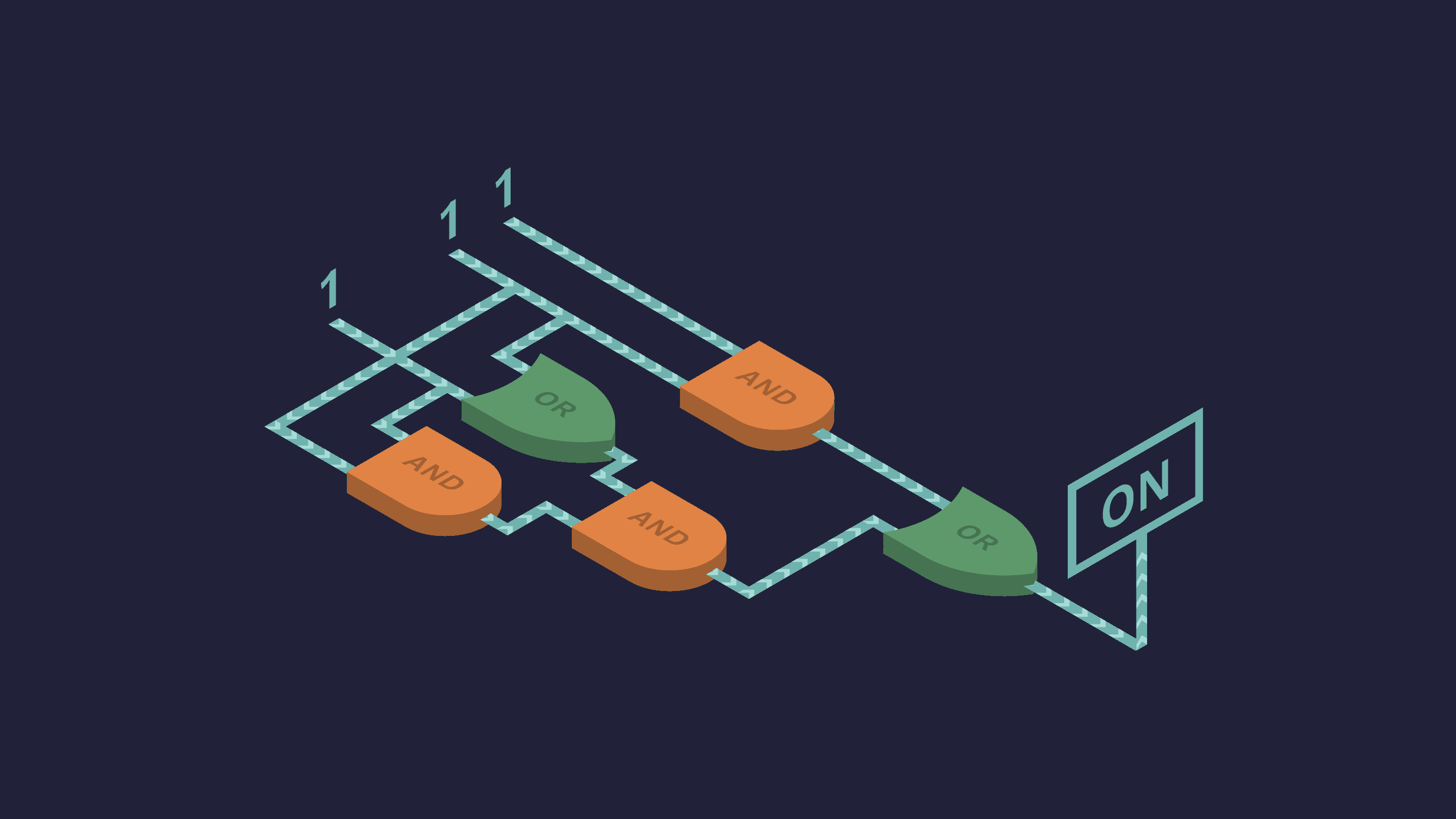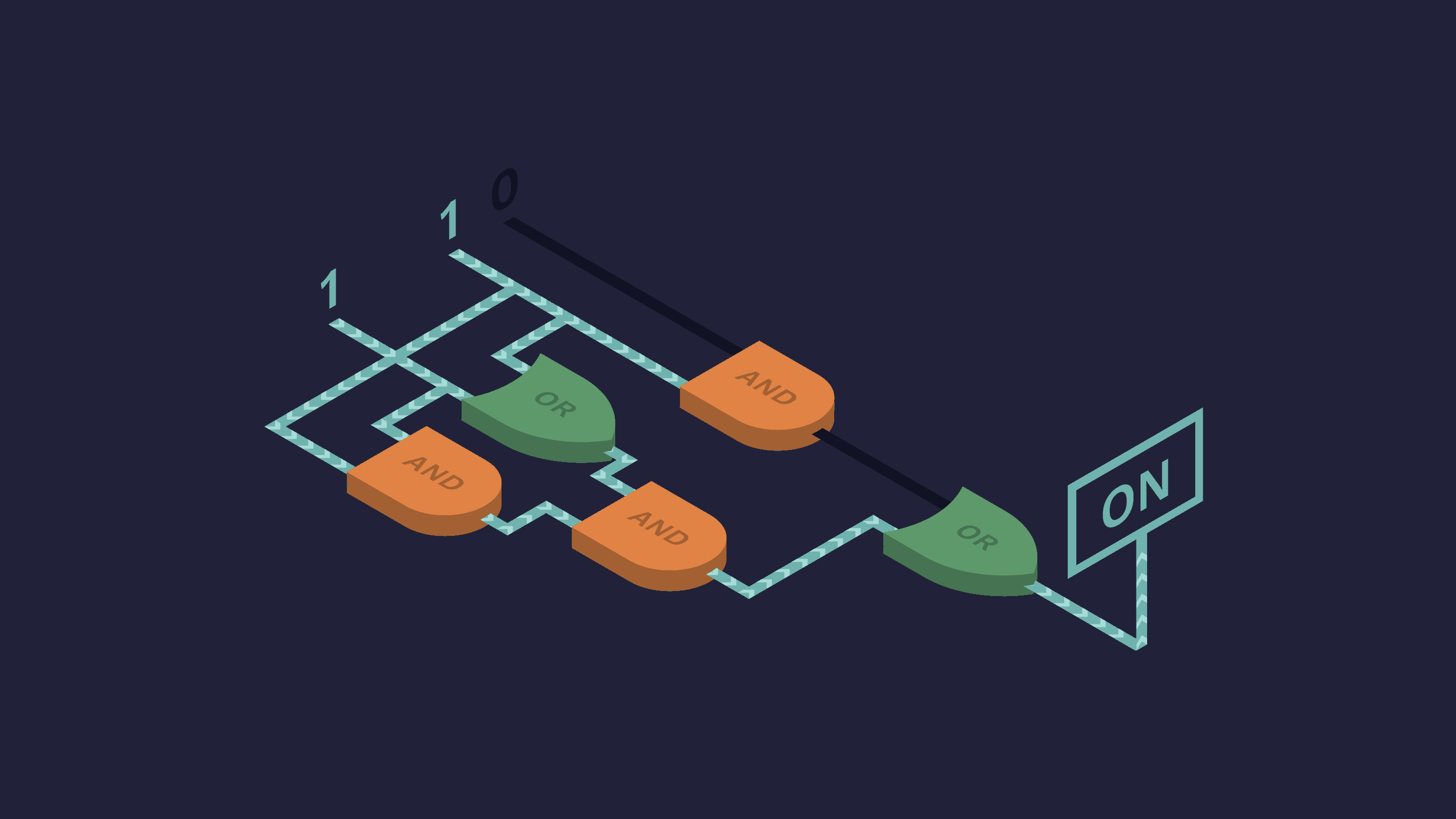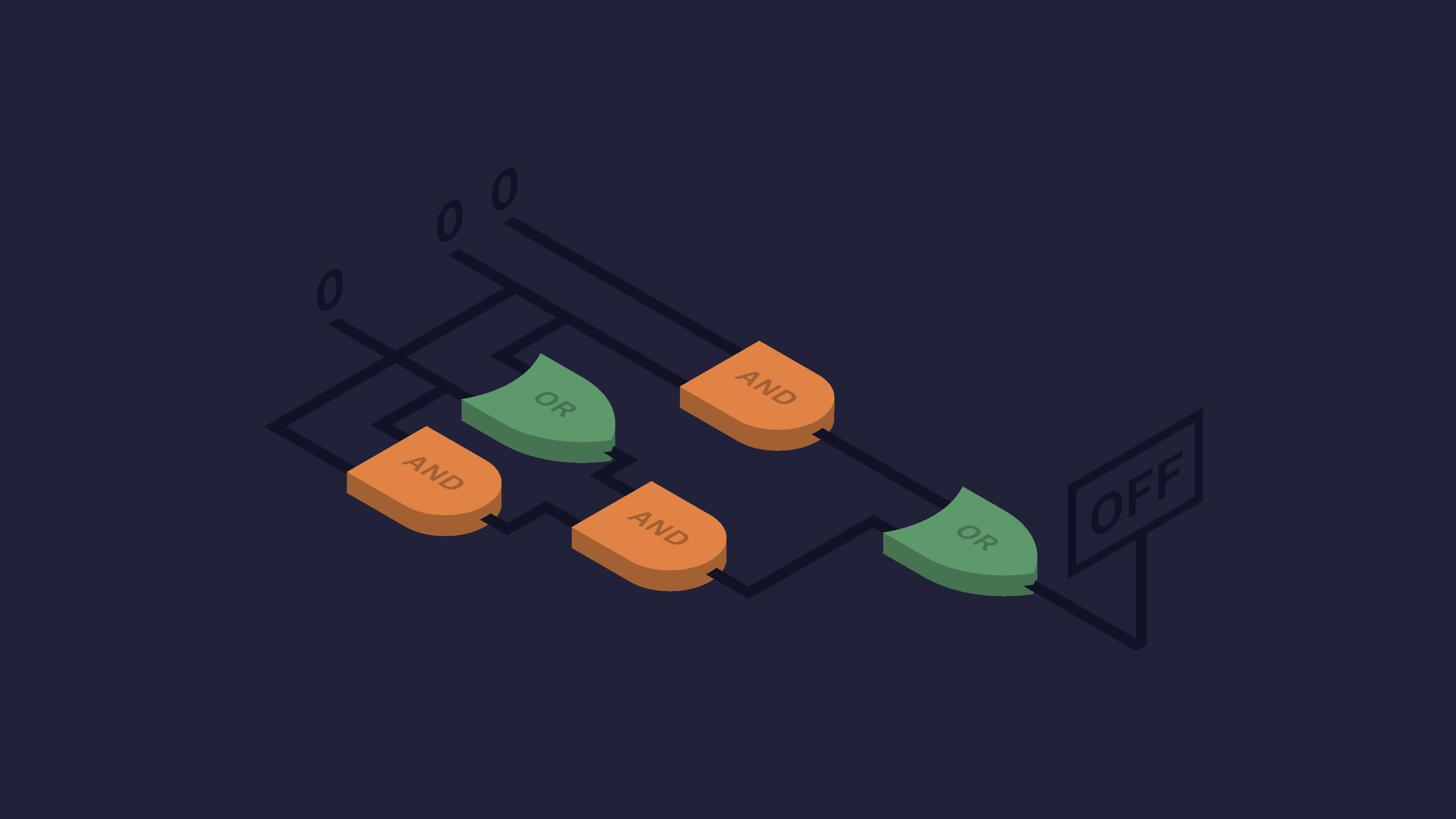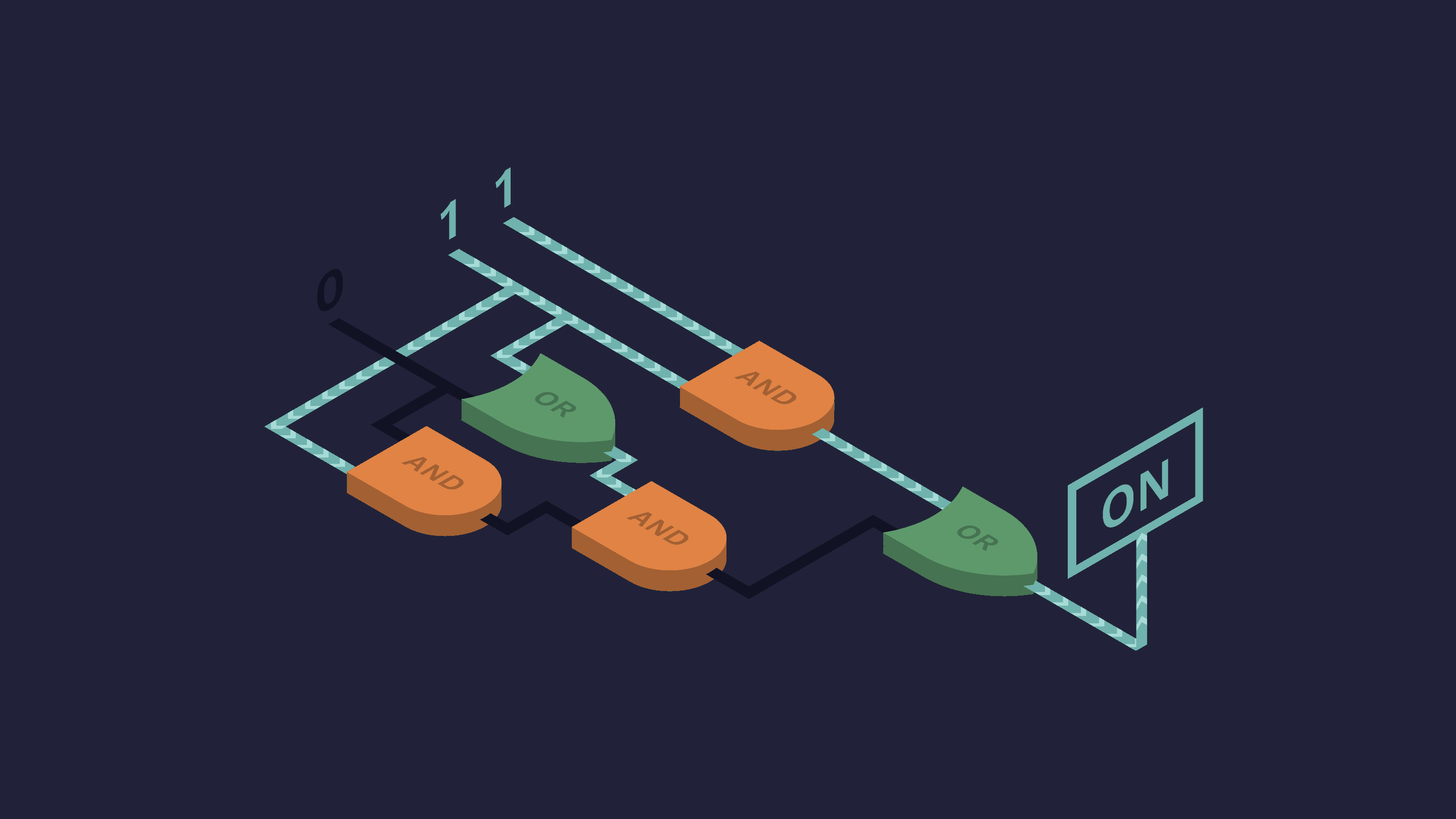
A gate-level circuit
(see footnote 1 for more info).
A second theory comes from classicist Pierre Vernant. Vernant argues that, beginning in the sixth century BCE, there was a new "positivist" type of reflection concerning nature. This is to say that thinkers weren't satisfied with divine explanations any longer. One example that Vernant gives is that thinkers were no longer satisfied with explaining cosmogenesis through sexual unions (Vernant 2006: 219). And so they emphasized theories that were more testable and arguable. They sought ways of explaining the world that were amenable to examination. According to Vernant, the special aspect of Greek thought isn't just that they could argue; it's that they would limit their argumentation to domains where argumentation might lead to a resolution. In other words, the Greeks moved away from superstition and supernatural explanations (where one explanation is just as good as another) towards explaining reality in physical terms (which is a step towards modern science; see Vernant 2006: 371-80).
Whatever the right way of characterizing the Greek miracle might be, it's clear that there was something special going on. And Aristotle's ideas are a part of this tradition. Sure, Aristotle had some ideas that were also very very wrong. In fact, some of his ideas actually impeded progress, as in physics. And we can talk about those if you want. But paired with that must be the acknowledgement that some of his ideas are nothing short of intellectual breakthroughs, breakthroughs that were expanded and improved upon by others, breakthroughs that shaped the modern world. For example, Aristotle's works on botany and zoology taught us how to systematize, an important step in scientific classification. Most important, I think, and the subject of this course, is his development of logic. It appears that, although logical principles were routinely used in argumentation, no one had sat down to codify them. Aristotle did.
“[W]e can say flatly that the history of [Western] logic begins with the Greek Philosopher Aristotle... Although it is almost a platitude among historians that great intellectual advances are never the work of only one person (in founding the science of geometry Euclid made use of the results of Eudoxus and others; in the case of mechanics Newton stood upon the shoulders of Descartes, Galileo, and Kepler; and so on), Aristotle, according to all available evidence, created the science of logic absolutely ex nihilo [out of nothing]” (Mates 1972: 206; interpolations are mine).


Important Concepts
Distinguishing Deduction and Induction
As you saw in the Important Concepts, I distinguish deduction and induction thus: deduction purports to establish the certainty of the conclusion while induction establishes only that the conclusion is probable.3 So basically, deduction gives you certainty, induction gives you probabilistic conclusions. If you perform an internet search, however, this is not always what you'll find. Some websites define deduction as going from general statements to particular ones, and induction is defined as going from particular statements to general ones. I understand this way of framing the two, but this distinction isn't foolproof. For example, you can write an inductive argument that goes from general principles to particular ones, like only deduction is supposed to do:
- Generally speaking, criminals return to the scene of the crime.
- Generally speaking, fingerprints have only one likely match.
- Thus, since Sam was seen at the scene of the crime and his prints matched, he is likely the culprit.
I know that I really emphasized the general aspect of the premises, and I also know that those statements are debatable. But what isn't debatable is that the conclusion is not certain. It only has a high degree of probability of being true. As such, using my distinction, it is an inductive argument. But clearly we arrived at this conclusion (a particular statement about one guy) from general statements (about the general tendencies of criminals and the general accuracy of fingerprint investigations). All this to say that for this course, we'll be exclusively using the distinction established in the Important Concepts: deduction gives you certainty, induction gives you probability.
In reality, this distinction between deduction and induction is fuzzier than you might think. In fact, recently (historically speaking), Axelrod (1997: 3-4) argues that agent-based models, a new fangled computer modeling approach to solving problems in the social and biological sciences, is a third form of reasoning, neither inductive nor deductive. As you can tell, this story gets complicated, but it's a discussion that belongs in a course on Argument Theory.
Food for Thought...
Alas...
In this course we will only focus on deductive logic. Inductive logic is a whole course unto itself. In fact, it's more like a whole set of courses. I might add that inductive reasoning might be important to learn if you are pursuing a career in computer science. This is because there is a clear analogy between statistics (a form of inductive reasoning) and machine learning (see Dangeti 2017). Nonetheless, this will be one of the few times we discuss induction. What will be important to know for our purposes is only the basic distinction between the two forms of reasoning.

Assessing Arguments
Validity and soundness are the jargon of deduction. Induction has it's own language of assessment, which we will only briefly cover next time. These concepts will be with us through the end of the course, so let's make sure we understand them. When first learning the concepts of validity and soundness students often fail to recognize that validity is a concept that is independent of truth. Validity merely means that if the premises are true, the conclusion must be true. So once you've decided that an argument is valid, a necessary first step in the assessment of arguments, then you proceed to assess each individual premise for truth. If all the premises are true, then we can further brand the argument as sound.4 If an argument has achieved this status, then a rational person would accept the conclusion.
Let's take a look at some examples. Here's an argument:
- Every painting ever made is in The Library of Babel.
- “La Persistencia de la Memoria” is a painting by Salvador Dalí.
- Therefore, “La Persistencia de la Memoria” is in The Library of Babel.
At first glance, some people immediately sense something wrong about this argument, but it is important to specify what is amiss. Let's first assess for validity. If the premises are true, does the conclusion have to be true? Think about it. The answer is yes. If every painting ever is in this library and "La Persistencia de la Memoria" is a painting, then this painting should be housed in this library. So the argument is valid.
But validity is cheap. Anyone who can arrange sentences in the right way can engineer a valid argument. Soundness is what counts. Now that we've assessed the argument as valid, let's assess it for soundness. Are the premises actually true? The answer is: no. The second premise is true (see the image below). However, there is no such thing as the Library of Babel; it is a fiction invented by a poet. So, the argument is not sound. You are not rationally required to believe it.
Here's one more:
- All lawyers are liars.
- Jim is a lawyer.
- Therefore Jim is a liar.
You try it!5


Decoding Validity
Closing Comments
As you might've noticed above, people need some time to calibrate their concept of logical consistency. It just means the statements can be true at the same time. Don't let blatantly false statements, especially politically charged ones, trip you up. If you do let yourself be tricked in this way, you can expect to have some problems on my test. You've been warned.
Also, be sure to distinguish between validity and soundness, a topic also covered in the video above. Validity is about the logical relationship between premises and conclusion, namely that the premises fully support the conclusion. Soundness is validity plus the premises actually being true. Finally, both validity and soundness are properties of arguments. Don't forget! Again, you've been warned.
Lastly, you might've noticed pictures of circles in this lesson. There'll be more to come. Why? You'll see...

FYI
Homework!
- Validity and Soundness Handout
- In this assignment, you will use the Imagination Method to assess arguments for validity; that is to say, you will simply think about the argument and attempt to figure out if it is valid or not.
- The Logic Book (6e), Chapter 1 Glossary
Footnotes
1. A basic building block of computers is a logic gate, which is functionally the same as some of the truth-tables we'll be learning in Unit II. Through a combination of logic gates you can build gate-level circuits, and out of gate-level circuits you build modules, such as the arithmetic logic unit (a unit in a computer which carries out arithmetic and logical operations.) Eventually, all the elements of a module were forced onto a single chip, called an integrated circuit, or an IC for short (see Ceruzzi 2012: 86-90). In the image you can see a gate-level circuit.
2. Not to get into theoretical physics here, but some students make the erroneous inference that because we split the atom, that means atomic theory is false. Not at all. It means, among other things, that physicists used the label "atom" too soon; they misapplied it by using in on objects that actually are divisible. But more importantly, quantum theory leads to the conclusion that there really is a lower limit to the size of things in the world, and they can't get any smaller than that lower limit. In a sense, Democritus was right. Rovelli (2017) refers to this granularity as one of the lessons learned from quantum theory.
3. It is important to note that different thinkers distinguish between deduction and induction in different ways (see Wilbanks 2010). Depending on how you distinguish these two, abduction is either a third form of reasoning or a type of induction. I'm agnostic on this matter. However, one of the main books I'm using in building this course is Herrick (2013), and it is his way of characterizing deduction/induction that we will be using. On the account that we're using, there's only deduction and induction, with abduction being a form of induction (see chapter 33, titled "Varieties of Inductive Reasoning", of Herrick 2013 to learn about his conception of abduction, also known as "inference to the best explanation").
4. Another common mistake that students make is that they think arguments can only have two premises. That's usually just a simplification that we perform in introductory courses. Arguments can have as many premises as the arguer needs.
5. This argument is valid but not sound, since there are some lawyers who are non-liars (although not many).

